Theoretical studies of a hydrogen abstraction tool for nanotechnology

Charles B. Musgrave1, Jason K. Perry1, Ralph C. Merkle2 and William A. Goddard III1

1: Materials and Molecular Simulations Center, Beckman Institute, California Institute of Technology, Pasadena, CA 91125, USA
2: Xerox Palo Alto Research Center, 3333 Coyote Hill Road, Palo Alto, CA 94304, USA

Nanotechnology 2 (1991)187-195.

This is a preliminary HTML version of the paper and might have errors.

Further information (links to related information and articles) is available at http://www.zyvex.com/nanotech/Habs/Habs.html.

Abstract

Processes that use mechanical positioning of reactive species to control chemical reactions by either providing activation energy or selecting between alternative reaction pathways will allow us to construct a wide range of complex molecular structures. An example of such a process is the abstraction of hydrogen from diamond surfaces by a radical species attached to a mechanical positioning device for synthesis of atomically precise diamond-like structures. In the design of a nanoscale, site-specific hydrogen abstraction tool, we suggest the use of an alkynyl radical tip. Using ab initio quantum-chemistry techniques including electron correlation we model the abstraction of hydrogen from dihydrogen, methane, acetylene, benzene and isobutane by the acetylene radical. Of these systems, isobutane serves as a good model of the diamond (111) surface. By conservative estimates, the abstraction barrier is small (less than 7.7 kcal mol-1) in all cases except for acetylene and zero in the case of isobutane. Thermal vibrations at room temperature should be sufficient to supply the small activation energy. Several methods of creating the radical in a controlled vacuum setting should be feasible. Thermal, mechanical, optical and chemical energy sources could all be used either to activate a precursor, which could be used once and thrown away, or alternatively to remove the hydrogen from the tip, thus refreshing the abstraction tool for a second use. We show how nanofabrication processes can be accurately and inexpensively designed in a computational framework.

1. Introduction

Mechanical positioning of reactive species can be used to convert mechanical energy to chemical energy to select between alternative reactions, or to provide activation energy. Mechanosynthesis is the employment of these mechanochemical processes to synthesize molecular structures [1]. Atomically precise mechanosynthesis promises to let us manufacture complex systems of molecular machinery. Examples include: self-replicating assemblers [2], molecular-scale surgical systems [2], computers made with molecular logic elements [3] and macroscopic machines made of diamond-like materials. Construction of such systems will require the ability to manipulate structure precisely on an atomic level. The great specificity of the chemical reactions required to synthesize designs with specific atomic structures should be achievable with mechanochemical tools capable of positioning the reactive moieties with sub-angstrom accuracy. Mechanochemistry allows alternative reaction transition states to be selected by manoeuvring the reactive species into a position where the chosen reaction has the smallest barriers. Such positional control requires that the tool exert forces and torques on the reactive molecule to move it over the potential energy surface of interaction with the workpiece.

Applying positional control to reactions will require that the tool have certain properties to make synthesis reliable, feasible and practicable. The tool must (i) have the proper chemical properties, (ii) be relatively small to reduce steric interactions with the workpiece, (iii) be capable of remaining chemically and mechanically stable under thermal motions and strains induced during positioning, (iv) be bound to a system that can transfer forces and torques to the reactive portion of the tool, (v) be selective between alternative reactions and (vi) be easily made. Molecular tips attached to atomic force microscope (AFM) tips, scanning tunnelling microscope (STM) tips or molecular robotic arms have been suggested [4].

Because construction of atomically precise machinery might require about as many unit operations as there are atoms in the system, it is important that reactions be fast. To increase the speed of reactions with moderate barriers, forces can be exerted between the workpiece and reactive species to effectively increase the pressure on the system, reducing the barrier height. Moderate reductions in the barrier heights lead to substantial increases in the reaction rate because thermal vibrations have an exponential Boltzmann probability of overcoming the reaction barrier. Mechanochemistry not only reduces the barriers by converting mechanical energy to chemical energy, but also maximizes the effective reactive concentration by positioning the reactive moieties to best advantage. These speed-enhancing steps together with having many mechanochemical machines working simultaneously can compensate for the loss of parallelism of solution-based reactions. Mechanochemical synthesis also increases the range of synthetic steps that can be used to build novel structures by the use of applied torques; a moiety attached to both the tool and the workpiece can be twisted, for example, to break pi-bonds [1].

Nanomachines made of complex specific arrangements of diamond-like material offer several advantages. First, diamond is light and stiff. Macroscopic machines could be made stronger and simultaneously much lighter, making such activities as air and space travel substantially more practicable. Moving parts of such machines would be lighter and therefore faster. Furthermore, hydrocarbons are abundant, making raw materials readily available and inexpensive. Stiffness is not only a desirable property of finished machines, but it is also useful during construction since the material surrounding the reactive site on the workpiece must be stiff. This allows it to withstand the compressive forces that might be needed to reduce reaction barriers, to withstand the tensile forces during moiety abstraction and to withstand torques applied to break pi-bonds.

Building machines of diamond will include manoeuvring hydrocarbons into reactive sites, torsion of structures, insertions into bonds and preparation of reactive sites by removing unwanted moieties to create radical sites. Abstraction of hydrogen is likely to be the most repeated step and common to building a wide range of molecular structures, including diamond-like structures. Highly reactive species are commonly thought to play a crucial role in the chemical vapour deposition (CVD) synthesis of diamond [5-7]. The abstraction of hydrogen via any of several radicals is one of the central mechanisms involved in the growth of diamond. It is not unreasonable, therefore, to expect that the atomically precise synthesis of diamond-like materials will utilize site-specific hydrogen abstraction via a radical as one of the main steps. Drexler has proposed using a molecular tip made of an ethynyl radical [1]


bound to a mechanical base on the tool (figure 1).

Figure 1. Acetylene radical hydrogen abstraction molecular tip attached to diamond-like material.
While many radicals exist, the desire for a simple, general, positionally accurate and sterically undemanding hydrogen abstraction tool can be used to narrow the search to a structure that (i) has a very high affinity for hydrogen, (ii) is not encumbered by surrounding groups, (iii) can be made part of an extended structure, which can be used as a 'handle' for positioning and can be attached to an STM or AFM tip, (iv) is mechanically and chemically stable during positioning, (v) is selective between alternative reactions such as abstraction of a neighbouring hydrogen or bonding to a nearby carbon atom and (vi) is easily made or regenerated. Perhaps the most natural structure in this regard is the ethynyl radical.

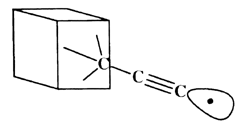
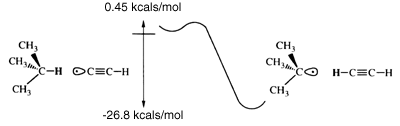
The C-H bond in acetylene is one of the strongest bonds to hydrogen; thus, the ethynyl radical formed by removing this hydrogen is likely to have a higher affinity for hydrogen than almost any other chemical structure. Further, the ethynyl radical can easily be incorporated into structures that provide a high degree of steric exposure. A structure resembling the propynyl radical, but with the carbon furthest from the radical site embed ded in an extended diamond-like structure (figure 1), provides both excellent steric exposure to the radical and a 'handle' for positioning the radical for the desired abstraction. Attachment of the tool to an STM or AFM tip may develop from technology designed for attachment of proteins to surfaces [4]. Drexler showed that the bending stiffness of an ethynyl-like tip attached to an adamantyl group is 6 N m-1 and can be increased to ~65 N m-1 by building up a surrounding collar [1]. If the reaction requires application of mechanical force to supplement thermal energy, then bending stiffness may need to be increased. Stiffness also is desirable to achieve selectivity. STM and AFM positioning is stable to more than sub-angstrom accuracy. However, bending modes of the ethynyl tip will be active at moderate temperatures. If during positioning of the tip, the bending of the radical and displacement of the AFM or STM relative to the work piece positions the reactive portion of the tip near a branched transition state, for example (one pathway leading to abstracting the neighbouring hydrogen), then selectivity is reduced. Drexler has shown that at worst at room temperature with a bending stiffness of 20 N m-1 and transition states separated by 1.2 Å the unwanted reaction rate is less than 10-12 times the rate of the target reaction [1]. Transition states between neighbouring hydrogens on the (111) surface of diamond are separated by 2.5 Å, and transition states for other possible reactions in diamond-like structures also generally exceed 1.2 Å, making mechanochemical reactions highly selective.

Table 1. Experimental bond dissociation energies (kcal mol-1).
R-HD0
H-H 102.3 [25]
CH3-H 105.1 [27]
(CH3)3C-H 93.2 [27]
C6H5-H 110.9 [27]
HCC-H 126.6 [11], 131.3 [9]
The strong C-H bond of alkynes (127-132 kcal mol-1 [8-12] should give large exothermicities and small barriers (rapid reactions) for alkynyl radical abstraction of hydrogen from weaker sp2 and sp3 hybridized C-H bonds (see table 1). The large exothermicity would also give a small reverse reaction rate constant. Compressive mechanical forces could be applied to supplement thermal energy in cases where the barriers are large; however, care must be taken so that the alkynyl radical tip does not bend away from the transition state. In the cases we study the barriers are such that this is not an issue.

Several methods of creating the radical should be feasible. The process of creating the radical should take place in an inert environment: vacuum, helium, or some other extremely non-reactive system would be appropriate. The activation energy required to create the abstraction tool could be provided from thermal, mechanical, optical, or chemical sources. There are two obvious approaches. In the first, a precursor compound is activated to create the abstraction tool. The tool is then used once and discarded. A second precursor would then be activated to abstract a second hydrogen. Thus, in a functioning system using this approach, a steady supply of the precursor would be required as well as a method for disposing of the 'used' abstraction tools.

In the second approach, the abstraction tool would be refreshed by the removal of the hydrogen after each use. Of course, the ethynyl radical was selected on the basis of its strong C-H bond, so removal of the hydrogen might at first seem paradoxical. However, there are several methods of solving this problem. One would be first to weaken the C-H bond, and then abstract the hydrogen from the abstraction tool using a weaker radical. Drexler [1] proposed that the C-H bond could be weakened by positioning a weak radical near the carbon atom. A second weak radical could then abstract the hydrogen from the tip.

An alternative to the 'attack by two weak radicals' strategy would be photoexciting the acetylene to obtain the pi pi* state, which would rearrange to the structure

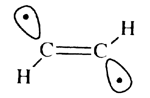
with a weak C-H bond and thereby allow removal of the hydrogen. Our primary concern is to analyse the energy barriers associated with hydrogen abstraction using alkynyl radicals to determine the feasibility of such a tool, rather than to analyse the methods of creating such a tool.

We model the chemically active site of the tool by the acetylene radical and determine the transition-state geometry and activation energy for transferring the hydrogen from several species: H2, CH4, C2H2, C6H6 and CH(CH3)3. The geometry of the various transition states can be used to position a working hydrogen abstraction tool for fast reaction and so as not to bend the tip. The barrier height itself can be used to calculate an abstraction rate at a given temperature and, thus, how long the abstraction tool must remain at the transition state until the probability that abstraction has occurred reaches a given value. Various levels of generalized valence-bond (GVB) and configuration-interaction (CI) ab initio calculations are used. To calibrate the accuracy of these calculations, we consider the abstraction barriers and transition states for hydrogen transfer between methyl and methane and for hydrogen transfer between H and H2 as compared to other theoretical and experimental results [13-15].

Figure 2. Schematic diagram showing the transition barrier and exothermicity of the acetylene radical abstraction of hydrogen from isobutane.

2. Results

Table 2. Barriers for the hydrogen abstraction reaction, R1-H + R2 --> R1 + H-R2, calculated at the CCCI optimized geometry (kcal mol-1).
R1-H-R2HFGVBCI-SCFCCCI DCCIHF*SD CIGVB*SD CI
H-H-Ha24.39.910.3 10.310.5(9.6)c 10.3(10.3)
CH3-H-CH3 34.927.829.8 17.522.5(19.5)20.4(18.8)
H-H-CCH11.68.0 5.40.84.5(3.2)3.3(2.7)
CH3-H-CCH14.68.6 10.2-2.9bb4.2(2.0)2.2(1.3)
(CH3)3C-H-CCH11.0 5.98.0-7.00.45(-2.78)  
C6H6-H-CCH18.312.0 14.3-0.77.7(4.1) 
HCC-H-CCH30.022.924.1 11.617.0(13.7)14.6(12.9)

The barrier to the acetylene radical abstraction of hydrogen from isobutane (sp3 carbon) is conservatively estimated to be less than 0.45 kcal mol-1 (figure 2). Reaction barriers calculated at various levels of correlation are shown in table 2. The barrier to abstraction of hydrogen by the acetylene radical from benzene (sp2 carbon) is estimated to be less than 7.7 kcal mol-1. The Hartree-Fock times singles and doubles configuration interaction (HF*SD CI) consistently overestimates the generalized valence bond times singles and doubles configuration interaction (GVB*SD CI) barriers, while the dissociation-consistent configuration interaction (DCCI) consistently underestimates the GVB*SD CI barriers. The GVB*SD CI barriers will be conservatively high due to a lack of a third diffuse p function, zero-point corrections and lack of more correlation of the valence electrons. Transition states were optimized at the correlation-consistent configuration interaction (CCCI) level (table 3). Although CCCI does not accurately predict activation barriers, it does accurately describe the transition-state geometries. For the largest cases, the number of spin eigenfunctions in the configuration-interaction (CI) calculation grows beyond our computational capabilities (table 4). This makes abstraction from benzene and isobutane at the GVB*SD CI level impracticable; however, the overestimated, yet small, barriers at the HF*SD CI level show that the acetylene radical hydrogen abstraction is feasible, thermal vibrations at room temperature providing sufficient energy to overcome the barriers. Table 5 shows the exothermicities for the various abstractions. There is little difference in the accuracy of the methods in predicting the exothermicities because all the methods describe bound states rather well. Note that the exothermicities are for reactions where the product radical species are not allowed to relax. This describes abstraction from surfaces where relaxation is constrained. Exothermicities for gas-phase reactions will be higher. The transition state is poorly described by many semi-empirical methods and by ab initio methods with insufficient electron correlation and small basis sets, and large variation of the predicted barriers can be seen in table 2.

Table 3. Transition-state geometries optimized at the CCCI level. See text for constraints on these geometries.
R1-H-R2 R1H bond length (Å) R2H bond length (Å) H-C-H anglea (deg)
H-H-H0.940.94 
CH3-H-CH31.36 1.36105.2
H-H-CC-H0.80 1.61 
CH3-H-CCH1.22 1.48105.5
(CH3)3C-H-CCH 1.21.5 
C6H5-H-CCH 1.241.42 
HCC-H-CCH1.281.28 

Table 4. Number of spin eigenfunctions in each of the Cl calculations. The numbers in parentheses are the number of spin eigenfunctions for the separated cases, R1-H + R2, where symmetry is broken.
R1-H-R2CCCI DCCIHF*SD CIGVB*SD CI
H-H-H191(386)191(386) 139(278)191(386)
CH3-H-CH34914(9829) 71666(143333)79428(158757) 310778(621164)
H-H-CCH216018234 1518953048
CH3-H-CCH9477 150557184851737651
(CH3)3C-H-CCH 216766958421675566 
C6H5-H-CCH17265 5873431514151 
HCC-H-CCH2697(5398)42201(84406) 55211(110314)221805(443182)

Table 5. Calculated exothermicities (kcal mol-1).
R1-H-R2HF GVBCI-SCFCCCIDCCI HF*SD CIGVB*SD CI
H-H-CCH33.931.6 31.830.130.0(27.5)a 29.9(28.1)
CH3-H-CCH28.9 28.427.029.2 26.9(25.5)26.8(25.4)
(CH3)3C-H-CCH 28.527.924.2 27.426.8(25.9) 
C6H5-H-CCH 18.718.215.4 18.918.3(18.0) 

3. Calculational details

Standard ab initio quantum-chemistry methods are employed and results are given for several levels of calculation. The simplest wavefunction used is the wavefunction in which each molecular orbital is doubly occupied. This single-configuration (one-determinant) Hartree-Fock (HF) wavefunction is the lowest-energy antisymmetrized n-fold product of molecular orbitals and should give a qualitative picture of the hydrogen abstraction reactions studied. HF will tend to overestimate the abstraction barrier since the radical-hydrogen stretching frequency is too high due to the poor description by HF of the bond breaking process (a doubly occupied orbital of the molecule must become two singly occupied orbitals for the fragments). This problem is remedied by using a GVB (generalized valence-bond) wavefunction [16], which allows each bond to be described with two singly occupied, overlapping orbitals leading to a proper description of dissociation. When solved for self-consistently, this calculation is termed a generalized valence-bond configuration-interaction self-consistent field (GVBCI-SCF) or equivalently a complete active space self-consistent field (CASSCF). Simply, all symmetry- and spin-allowed configurations of three active electrons in three orbitals are generated. These electrons are the radical of the reactant, the hydrogen and the radical of the product. All other orbitals (considered inactive) are doubly occupied as in Hartree-Fock. It is found that three configurations are all that is necessary to describe the transition state adequately. These are the dominant configuration (with the Hartree-Fock occupations of the orbitals) and the single and double excitations of the electrons in the doubly occupied R1-H-R2 bonding orbital to the empty R1-H-R2 antibonding orbital. The R1-R2 antibonding orbital (with a node at the hydrogen centre) is singly occupied in all three configurations. While this level of calculation includes the most important correlation, it will still tend to overestimate the abstraction barrier and, thus, will only serve as a zeroth-order wavefunction for large CI (configuration-interaction) expansions, which will account for additional dispersion.

Ideally, we would like to do a CI calculation in which all single and double excitations of the valence electrons are made into the virtual orbitals with reference to the three most important configurations describing the abstraction. This type of multi-reference CI (called a GVB*SD CI) has been well established in approximating results of complete CI calculations [17]. However, this CI has not been carried out for the largest cases, abstraction of hydrogen from isobutane and benzene by the acetylene radical. Thus we have considered some smaller CI calculations, which will do a good job in approximating the barriers for the larger CI. The first of these is the CCCI wavefunction [18, 19]. It involves making all single and double excitations of the active electrons and all single excitations of the other valence electrons into the virtual space relative to the three GVB references, or simply GVB*(SDactive + Svalence). The second CI, called a DCCI (dissociation-consistent configuration interaction), will add the double excitations, which are the product of a single excitation of an active electron and a single excitation of a valence electron, or GVB*(SDactive + Sactive*Svalence + Svalence). The third CI does all single and double excitations of the valence electrons (active and inactive) relative to only one reference, a calculation called HF*SD CI (or equivalently one-reference SDCI). Table 4 shows the sizes of the CI expansions in terms of the number of spin eigenfunctions (SEF) for each of the systems studied. The HF*SD CI already approaches the limits of our programs (about two million SEF) in the cases of isobutane and benzene, for which the GVB*SD CI is not possible. In all other cases, however, the GVB*SD CI are of small to medium size and will serve as benchmarks to calibrate the accuracy of the smaller CI.

The standard basis sets of Dunning and Huzinaga are used [20,21]. Their double-zeta contraction of the 9s5p set is used on all carbons, with the addition of one set of d polarization functions (Zd = 0.75). On the active carbons, diffuse s and p functions (Zs = 0.0474 and Zp = 0.0365) are also added. For active hydrogens or hydrogens bound to active carbons (in the case of methane), the triple-zeta contraction of the 6s set is used, supplemented with a p polarization function (Zp = 0.60). For all other hydrogens, the double-zeta contraction of the 4s set is used, scaled by a factor of 1.2.

Figure 3. Geometries for the transition states.

The basic geometries of the various systems studied are illustrated schematically in figure 3. The geometries will be optimized at the CCCI level. The orbital optimization at the GVBCI-SCF level is the most time-consuming step, so this CI will be a simple correction to that wavefunction. It would be impracticable to do the geometry optimization at a higher-level CI. It would also be impracticable to do a full geometry optimization, so certain constraints are assumed. Namely, only the parameters relevant to the description of the hydrogen abstraction (R1H and R2H or combinations thereof) will be optimized. In the case of abstraction from methane (by the methyl radical or by the acetylene radical), the H-C-Habs bond angle is also optimized since this angle changes from 109.5° for methane to 90° for the methyl radical. For isobutane, we would expect a small relaxation from a tetrahedral C-C-Habs bond angle to something more planar at the transition state and in the radical species. But Page and Brenner [22], in their work on abstraction of hydrogen from isobutane by atomic hydrogen, found that full relaxation of the t-butyl species reduced the abstraction barrier by only 1.7 kcal mol-1 at the GVBCVI-SCF level. GVBCI-SCF level. However, since the goal of this work is to show the feasibility of using an alkynyl radical tip as a hydrogen abstraction tool, a conservative overestimate of the abstraction barriers is acceptable. So the C-C-Habs bond angle is fixed to 109.5° in these calculations. All other radicals are expected to show little or no relaxation and are fixed to the experimental values of their hydrogen bound counterparts.

All calculations are run with the GVB [23] and MOLECULE-SWEDEN (an electronic structure program system written by Almlof et al [24]) suites of programs on the Caltech group's Alliant FX/80 and FPS5OO.

4. Discussion

4.1. H-H-H

A great deal of theoretical work has been done on this system [15] and, owing to its simplicity, it provides a good test of our hydrogen basis set and, to a lesser extent, our methods. While the calculated equilibrium bond distance in H2 compares favourably with experiment (0.74 Å vs. 0.74144 Å [25]), the calculated dissociation energy for H2 (De) is 105.4 kcal mol-1 compared with the experimental 108.6 kcal mol-1 [25]. This discrepancy of 3 kcal mol-1 is chiefly due to the lack of a second p polarization function. In contrast, the transition state is well described by the GVB*SD CI (in this case only, the CCCI, DCCI and GVB*SD CI are equivalent since there are no valence electrons in addition to the three active electrons). The optimized geometry has a H-H distance of 0.94 Å (compared to Liu's value of 0.930 Å [15]) and a barrier of 10.3 kcal mol-1 (compared to Bauschlicher's value of 9.56 kcal mol-1 using a large atomic natural orbital (ANO) basis set [15]). The geometries for all the systems studied are listed in table 3 and the abstraction barriers are listed in table 2. An error of less than 1 kcal in the barrier is adequate for the calculations at hand, particularly since the barrier is overestimated. It should be noted, however, that the Hartree-Fock barrier is well off the mark at 24.3 kcal mol-1 and that the apparently good result at the GVBCI-SCF level (9.9 kcal mol-1) is primarily due to the weak H-H bond strength (87.5 kcal mol-1) at this level. The HF*SD CI number including the Davidson correction is in fortuitous agreement with the reference barrier height of 9.56 kcal mol-1. This is rather symptomatic of the Davidson correction, which can often overestimate the contributions from additional correlation.

4.2. CH3-H-CH3

The methyl-methane hydrogen transfer reaction is perhaps more representative as a test case of the systems in which we are most interested. There has been less theoretical work done on this system [14] but a reliable experimental number for the abstraction barrier of 14.2 kcal mol-1 [13] gives a good benchmark for us to work with. Theoretical investigations into this reaction have not been successful in obtaining quantitative accuracy in the barrier height. The best calculations overestimate the barrier by 5-6 kcal mol-1. Part of this is due to some assumptions made in the calculations, namely the neglect of zero-point corrections, the Born-Oppenheimer approximation and temperature effects. However, the sum of these effects should only lower the theoretical activation energy by 1-2 kcal mol-1(see Sana et al [14]). Our results agree well with previous theoretical work. The optimized transition-state geometry is virtually identical to the full gradient optimized structure of Wunsch et al [14], which was done at the Hartree-Fock level. The calculated barrier is 20.4 kcal mol-1, higher than experiment by 6.2 kcal mol-1. Test calculations with a large ANO basis set [26] only lowered the barrier to 19.2 kcal mol-1, indicating that the discrepancy between theory and experiment is probably a correlation problem rather than a basis set problem. The importance of ionic terms such as (CH3-H+--CH3) are probably underestimated in the CI calculations owing to biases against anionic states and would require additional correlation of the non-active valence electrons. This could be a formidable task even for such a small system and would not be possible with our current code for the larger cases we wish to study. However, again, since these factors all tend to lead to an overestimate of the barrier height, the results for abstraction of hydrogen by the acetylene radical can be considered a conservative upper limit to the actual barrier height. These calculations on the methyl- methane system also offer a comparison of the smaller CI to the GVB*SD standard. We find the CCCI result (29.8 kcal mol-1) to be comparable to the GVBCI-SCF number (27.8 kcal mol-1), being slightly higher due to the stronger C-H bond at the CCCI level (113.2 kcal mol-1 vs. 97.6 kcal mol-1 at the GVBCI-SCF level and 107.2 kcal mol-1 at the GVB*SD CI level). This indicates that correlation of the non-active electrons is important in obtaining quantitative accuracy for the hydrogen abstraction barriers. The DCCI, which includes only limited correlation of the inactive electrons, underestimates the GVB*SD CI barrier by 2.9 kcal mol-1. Alternatively, the HF*SD CI, which sacrifices some of the active electron correlation, overestimates this barrier by 2.1 kcal mol-1. The combination of these two CI calculations should offer an upper and lower limit to the GVB*SDCI for those large cases where that CI is not feasible.

4.3. H-H-CCH, CH3-H-CCH, C6HH-CCH and HCC-H-CCH

Results of calculations on these systems underscore the results of methyl-methane. In particular, Hartree-Fock greatly overestimates the activation energies, GVBCI-SCF and CCCI offer some improvement but still overestimate these barriers, and DCCI and HF*SD CI bracket the results of the GVB*SD CI. In the case of abstraction from methane and benzene, we found that the geometries were most conveniently optimized by using the coordinate system R1H + R2H and R1H - R2H. In the case of abstraction from H2, it was easier to optimize the transition state in terms of the coordinates R1H and R2H. This was probably due to the fact that the barrier was small at the CCCI level and that it occurred quite early, with only an 8% increase in the H-H bond length. To a large degree the barrier height and the position of the barrier are determined by the exothermicity of the reaction. Other properties, such as the polarizability of the bonds, play a role as well. The largest barrier (and latest transition state) was for abstraction from acetylene, with an activation energy of 14.6 kcal mol-1. This is as expected, since this particular reaction is thermoneutral. The calculated exothermicities of the other reactions are listed in table 5 (see also table 1, for the experimental bond dissociation energies). H2 and CH4 are the most exothermic and have the smallest barriers. These barriers may be considered negligible as the calculations on H + H2 and methyl-methane showed the numbers to be overestimated. Abstraction from benzene is less exothermic and shows a small but non-negligible barrier. In addition the phenyl-H bond is stretched 14% at the transition state in comparison to an 11% stretch of the methyl-H bond. All of these results correlate with the exothermicities of the reactions.

4.4. (CH3)3C-H-CCH

Finding the transition state for abstraction from iso-butane proved to be quite difficult. The potential energy surface has many of the same features as that of H-H-CCH, in particular, a small, early barrier that leads to non-quadratic behaviour in the region of the saddle point. Owing to the computational costs of these calculations, it was necessary to sacrifice some accuracy in order to find the transition state. In the end, the values of R1H = 1.2Å and R2H = 1.5Å are in agreement with results for abstraction from methane and benzene by the acetylene radical. The large CI calculations strongly indicate that there is no barrier for abstraction of hydrogen, the more conservative number giving a barrier of only 0.45 kcal mol-1. This again correlates with the large exothermicity of this reaction, which is calculated from snap bond energies. If one considers that the t-butyl group should relax somewhat at the CCCI transition state and, thus, lower the energy of the barrier still, the argument for the absence of a barrier becomes even more persuasive. Since this system is a good model for the hydrogenated diamond (111) surface C-H bond, we conclude that no barrier exists to abstraction of hydrogen from this surface by acetylene. Barriers on other surfaces of diamond are probably non-existent or negligibly small.

4.5. Abstraction from acetylene

Table 6. Calculated relevant energetics of ground-state acetylene and the excited-state triplet (kcal mol1).
 HFGVBCI-SCF MR*SD CI
Te(3Bu <-- 1E+g) 72.392.090.2(87.6)
De(1E+g HCC-H)116.5 122.3131.9(132.0)
De(3Bu HCC-H) 44.230.341.7(44.4)

Now that it has been established that an alkynyl-tipped hydrogen abstraction tool would be able to abstract hydrogen from diamond surfaces with little or no thermodynamic hindrances, it would be desirable to find a method for removing the hydrogen from the tip. A simple alternative, but less elegant strategy is to make a new tip for each abstraction and dispose of the tool after use. What makes the acetylene good at abstracting hydrogen is the strength of its C-H bond. However, this bond is quite weak in the 3Bu excited state (see table 6). We calculate a bond strength of 41.7 kcal mol-1 doing a GVBCI-SCF in which all 10 valence electrons are active in 10 orbitals, followed by a multi-reference times singles and doubles configuration interaction (MR*SD CI) in which all configurations in the GVBCI with coefficients < 0.05 are chosen as references. In the case of the triplet excited state, there are four references and, in the case of dissociated H + CCH, there are six references. The geometry for the excited state is optimized at the MR*SD CI level. The molecule is not linear in this state, having a C-C-H bond angle of 132.0°. The C-C bond length also increases to 1.38 Å from 1.20 Å for the ground state, reflecting the double bond character of this bond. The weakening of the C-C bond in the excited state leads directly to the weakening of the C-H bonds, as the triple bond character can be restored upon dissociation of one of the C-H bonds. The weakening of the C-H bond leaves the acetylene prone to abstraction, making it easy to remove the hydrogen and refresh the tip. So photoexcitation of the alkynyl tip from its ground state to the 1Bu excited state, followed by relaxation to the triplet would facilitate the breaking of the tip-hydrogen bond. Drexler also made an alternative proposal for removing the hydrogen from the tip [1].

5. Conclusion

We model the abstraction of hydrogen from H2, CH4, C2H2, C6H6 and CH(CH3)3 by the acetylene radical using accurate CI ab initio quantum-chemistry techniques. From our results, conservative estimates show that the reaction barriers for abstraction from sp3 hybridized carbons are negligible, or zero for the case of isobutane. The barriers are small for sp2 hybridized carbons and slightly larger for sp hybridized carbons. Therefore, abstraction tools based on ethynyl radical molecular tips should reliably and rapidly abstract hydrogen from most carbon structures at moderate temperatures. We also find that the hydrogen bond to the pi-pi* excited enthynyl tip is relatively weak, and therefore can be broken to refresh the tip. We have also shown how nanofabrication processes can be accurately and inexpensively designed in a computational framework.

Acknowledgments

We gratefully acknowledge the useful discussions with K Eric Drexler, Siddharth Dasgupta and Erik P Bierwagen. CBM was supported by a Department of Defense National Defense Science and Engineering Grant (NDSEG) fellowship and JKP was partially supported by a BP America fellowship. This research was partially supported by the Xerox Corporation. The facilities of the Materials and Molecular Simulations Center were supported by grants from NSF (NSF-CHE-9100284) and ONR/NRL, and by grants from Allied-Signal, BP America, Asahi Chemical, Asahi Glass, General Electric, General Motors, Chevron and Xerox.

References