A Proof About Molecular Bearings

This paper is an updated and revised version of the paper first published in Nanotechnology, Volume 4, 1993, pages 86-90.

Further information about nanotechnology is available at http://www.zyvex.com/nano.

Abstract

Molecular bearings are likely to be as ubiquitous in future molecular machines as conventional bearings are in today's macroscopic machines. The ability to design molecular bearings will therefore be crucial. In molecular bearings made from a shaft with m-fold symmetry and a sleeve with n-fold symmetry, we prove that the potential energy of the bearing as a function of the rotational position of the shaft within the sleeve will be periodic, with a period of GCD(m,n)/ (m*n). This result continues to hold true even when the shaft and sleeve are jointly minimized, so that the abstract perfect symmetries of the shaft and sleeve are marred by the perturbations in structure each induces in the other. If the period is sufficiently short, e.g., if a small rotational change drives the bearing from one minima to the adjacent minima in the potential energy function, then the barrier height will be small and the bearing will be able to rotate without difficulty.

Introduction

Molecular bearings will be a fundamental component of many molecular mechanical devices. Previous work on micromachine bearings has produced poor results, both experimentally and in theory[2, 10]. Lubricating the bearing is of little use, for the viscosity of the lubricant effectively increases as the scale is reduced. As we move into the molecular size range, individual lubricant molecules can be viewed more as grit. However, unlubricated micromachine bearings also have poor performance. Friction is high, and problems of wear become increasingly severe as bearing size is decreased: wear rates that are acceptable in a macroscopic bearing will result in the rapid disintegration of small bearings. Proposals for non-contact bearings have suffered from other problems, including low load handling ability.

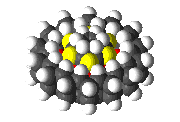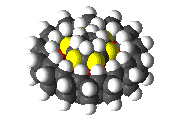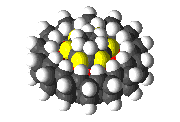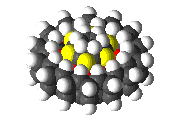
Drexler[1, 5] pointed out that these problems can be solved by the use of atomically precise bearings. The structure of a simple molecular bearing might be defined by taking two flat sheets of some material, bending them into two hoops of slightly differing diameter, and inserting the smaller hoop into the larger hoop. (This is a description, not necessarily a manufacturing method). Such a bearing is illustrated in figure 1 which shows a simple bearing made of two graphite sheets, with hydrogen terminating the dangling bonds that would otherwise occur at the edges of the sheets. The ability to synthesize this specific bearing has not been demonstrated, so the present analysis is theoretical (although there has been recent experimental work on structures that are generally similar[7]). Some system-level contexts in which molecular bearings would be useful have been discussed in Nanosystems.

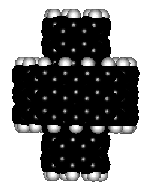Figure 1.

Figure 1, end view.

Molecular bearings can be "run dry", as first suggested by Feynman[4]. If the surfaces are atomically precise, the problem of wear can be avoided. Such an atomically precise surface is either perfect, or is broken because one or more atoms are out of place. If, however, the forces on the surface atoms are insufficient to dislodge them (and because the surfaces are atomically precise, the load can be distributed quite evenly) then the wear on the bearing (in the conventional sense) becomes zero. Bearing lifetime is no longer limited by wear. In our graphite bearing, continued rotation of the shaft within the sleeve will not cause the molecular structure to spontaneously disintegrate.

Friction in a macroscopic bearing is caused by surface irregularities. Typical macroscopic objects have rough surfaces (when viewed from the atomic scale), and these grind over each other. This process dislodges particulates and produces significant changes in the structure of the two surfaces. In an atomically precise molecular bearing, this need not occur and so friction in the conventional sense need not exist. However, while conventional friction is not a problem, it might still be the case that the bearing has certain preferred positions. That is, when we rotate the shaft with respect to the sleeve the potential energy of the system will increase and decrease periodically. While this process need not dissipate significant amounts of energy, it does mean that the "bearing" will have certain preferred orientations. If the change in potential energy is sufficiently large, the bearing would "stick" at certain preferred orientations and fail to rotate.

Graphite is used as a lubricant, and so one might expect that the graphite bearing illustrated in figure 1 would have low "static friction" for this reason alone. The bearing illustrated in figure 2 consists of two sheets of 111 diamond that have been bent into two hoops. Again, the smaller hoop has been inserted into the larger hoop to produce the bearing. The structure is chemically very simple. It uses only two atom types: carbon and hydrogen; and only two bond types: carbon-carbon single bonds and carbon-hydrogen bonds. In this bearing it is perhaps less obvious that the barrier to rotation should be small, although this is the case.

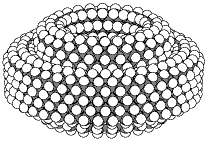Figure 2.

A Solution

A solution to this problem, first proposed by Drexler[1], is to make the shaft and sleeve with m- fold and n-fold symmetry, respectively, where the GCD (Greatest Common Divisor) of m and n is small. In this case, the shaft will have no strongly preferred position with respect to the sleeve. Thus, the force required to cause rotation of the shaft with respect to the sleeve will be minimal. Molecular mechanics models of such bearings have shown that the potential energy as a function of rotational position can indeed be very nearly flat. For example, the graphite bearing of figure 1 has m=7 and n=15, for a periodicity of 1/105. The barrier height between adjacent minima, modeled with the Dreiding II force field[8] as implemented by MSI in PolyGraf, is less than 0.001 kilocalories per mole. The bearing of figure 2 has m=13 and n=20, for a periodicity of 1/260. The barrier height, modeled with the MM2 force field[9] as implemented by MSI in PolyGraf, is less than 0.004 kilocalories per mole. By way of comparison, thermal noise at room temperature is about 0.6 kilocalories per mole. These numbers might be somewhat in error due to roundoff; it is possible that the true barrier heights are significantly lower than given here. The qualitative nature of the conclusion -- e.g., that the barrier to rotation is small -- is unaffected by the kinds of errors that might reasonably be expected in either the empirically derived force fields or the minimization process.

While this result is intuitively obvious, it is sufficiently important that it warrants a closer and somewhat more formal examination. Bearings are, after all, an essential component in conventional macroscopic machines, and it is reasonable to expect they will have equal importance in molecular machines. The conditions that must be met to insure adequate performance of molecular bearings are therefore worth more careful examination.

Rigid Structures

We will first examine the problem by adopting the "rigid atom" approximation. In this approximation, the shaft and sleeve are assumed to be perfectly symmetrical. This assumption is clearly false, for in a real structure they will somewhat deform each other, thus breaking the symmetry. However, the idealized case will serve as a basis for the later analysis of the more realistic case in which the geometry of the shaft and sleeve are allowed to interact.

We shall assume that the shaft has m-fold symmetry and angular orientation Q; while the sleeve has n-fold symmetry and angular orientation F. 

                 symmetry   angular position

    shaft        m-fold                Q

   sleeve        n-fold                F
We assume that the shaft and sleeve have perfect symmetry and are initially positioned with Q=Q0 and F=F0.

We first note that rotation of the shaft by q/m or the rotation of the sleeve by r/n (for arbitrary integers q and r) produces a structure which is physically isomorphic with the original structure in which Q=Q0 and F=F0. Now, the relative angular rotation, R, between the shaft and the sleeve is simply Q-F. That is, by definition:

(1) R = Q - F

and by the symmetries of the shaft and sleeve, a bearing B1 in which R1 = Q1 - F1 is isomorphic to the initial bearing B0 in which R0 = Q0 - F0 when there exist two integers q and r such that:

(2) Q1 - Q0 = q/m

and

(3) F1 - F0 = r/n

(we define a single 360 degree rotation as having the value 1. Thus, a rotation of 1/4 would be, by definition, equal to 90 degrees).

(1), (2) and (3) imply B1 will be isomorphic with B0 when R1-R0 = (Q1 - F1) - (Q0 - F0) = (Q1 - Q0) - (F1 - F0) = q/m - r/n

or

(4) R1-R0 = (q*n - r*m)/(m*n)

There are integers i and j such that

(5) GCD(m,n) = i*m + j*n

(This is a theorem from elementary number theory. See, for example, [6] page 4).

By setting q=j and r=-i, equation (4) becomes:

(6) R1-R0 = (j*n + i*m)/(m*n)

or

(7) R1-R0 = GCD(m,n)/(m*n)

Thus, a relative angular rotation of GCD(m,n)/(m*n) produces a structure which is isomorphic with the original. By multiplying equation (5) by an arbitrary integer, we can obtain the result that a bearing B1 is isomorphic to a bearing B0 if

(8) R1-R0 = p*GCD(m,n)/(m*n) for any integer p

Of course, isomorphic structures (which differ only in their spatial orientation) must necessarily have the same potential energy. If we let E(R) be the function describing the potential energy of the system as a function of relative angular rotation, then we have just proven that:

(9) E(R) = E(R+p*GCD(m,n)/(m*n)) for any integer p

i.e., we have proven that the energy of the system is periodic, with period GCD(m,n)/(m*n). By selecting m and n so that GCD(m,n) is small, we can effectively create a short period. In particular, if GCD(m,n)=1, i.e., m and n are relatively prime, then the period will be 1/(m*n).

Realistic Molecular Structures

This, of course, applies only to idealized rigid shafts and sleeves. What of real shafts and sleeves, in which the sleeve can relax and adjust to the shaft, and the shaft can relax and adjust to the sleeve, thus breaking the symmetry?

Here, too, we can prove a similar result. In our proof that idealized rigid bearings were periodic with period GCD(m,n)/(m*n), we proved that changing the relative angular rotation of the bearing by GCD(m,n)/(m*n) was equivalent to permuting the labels of the atoms in the bearing. In a real bearing it is also possible to apply the same permutation to the atoms, again resulting in a rotation of GCD(m,n)/(m*n). Because the structures differ only in the labels, and are physically isomorphic, they will of course have the same energies. Thus, real bearings also have an energy which is periodic with period GCD(m,n)/(m*n).

While generally true, this observation can be false under special circumstances. It is normally possible, if the atoms in the bearing are labeled, to determine the relative angular rotation of a bearing to within multiples of whole rotations. However, this is not strictly a logical necessity. If the bearing is composed of a collection of "black hole" atoms that swallow everything, then the bearing will lose all symmetry when it is relaxed, because the "black hole" atoms will collapse into a single point. This point will have no symmetry at all, and will have only a single minima (not (m*n)/GCD(m,n) distinct minima). In real structures that are chemically stable, this is unlikely to occur.

What Was Not Proven

Note that this proves only that (m*n)/GCD(m,n) isomorphic and distinct instances exist, and have equivalent energies and equi-spaced R values. It does not prove that these are the only structures which have similar R values. In a trivial sense, we know that other structures with different energies exist, for minor perturbations of the bearing structure will result in minor perturbations of the energy without disturbing R. However, a more significant problem arises because two different local minima might exist which have the same R value but different energies. This possibility, that the bearing might have two stable states (two minima) with the same R value, is not ruled out by our proofs.

An example of such a bad bearing might be taken from the "Wheel of Fortune." In this structure, the shaft might have m equally spaced nails, while the sleeve might have n equally spaced sticks that insert into the spaces between the nails. When the wheel is spun, the sticks will clatter against the nails. As a given nail is on the very verge of passing a given stick, a slight forward motion of the shaft will cause the stick to clatter down behind the nail. A slight backwards motion of the shaft will then fail to restore the stick to its proper place, thus resulting in two distinct energy minima for the same relative angular rotation R.

This kind of "popping" or "snapping" action must be avoided for the bearing to operate smoothly. In general, if the atoms along the surface of the bearing are well anchored with respect to motion around the bearing, this kind of problem should not occur. Molecular mechanics modeling of proposed bearing structures can be used to determine if this kind of situation exists.

Further, although E(R) is periodic, this does not by itself provide any guarantees about the size of the barrier that separates two adjacent minima. However, in reasonable situations in which relatively prime and reasonably large values of m and n are used, the displacement caused at the bearing surface by an angular rotation of 1/(n*m) will be a modest fraction of an angstrom. If the shaft repeats its structure every 2 or 3 angstroms (as would occur if the inner surface were graphite), and if the sleeve has an n value between 10 and 20, then 1/(m*n) corresponds to a displacement of about 0.1 to 0.2 angstroms. The normal spacing between sheets in graphite is about 3.4 angstroms, and we can reasonably assume that the spacing between the outer atoms of the inner bearing and the inner atoms of the outer bearing will not be greatly smaller than 3 angstroms. There should be no abrupt changes in energy and force as the atoms in the shaft move 0.1 to 0.2 angstroms with respect to the atoms in the sleeve that are some 3 angstroms away, particularly in surfaces (such as graphite) that were deliberately chosen to be as smooth as possible. Larger values of m and n would further reduce this.

We have also not examined the behavior of the bearing under load. Some analysis of this general problem has been done by Drexler[1, 5], who showed that molecular bearings can be designed with good performance even when relatively large loads are applied. Again, molecular mechanics models can be used to determine the behavior of a specific bearing under load.

A Further Improvement

It is sometimes possible to obtain a further factor of 2 in frequency, e.g., it is possible to obtain bearings with a period of GCD(m,n)/(2*n*m). This will occur when the following symmetry conditions exist. Consider a mirror plane that is perpendicular to the axis of the bearing, and which cuts through the center of the bearing. Either the shaft, the sleeve, both, or neither might be symmetrical with respect to reflection in this mirror. Assume that the shaft is symmetrical with respect to reflection in the mirror plane, and that the sleeve is not. Further assume that, while the sleeve is not symmetric in the mirror plane, that it is symmetric when (1) reflected in the mirror plane and then (2) rotated by 1/(2*n). This occurs, for example, in the bearing of figure 1. Under these conditions, if we reflect the entire bearing through the mirror plane then the shaft will be unchanged, while the sleeve will effectively have been rotated by 1/(2*n). The preceding observations will now hold, but substituting 2*n for n; this implies E(R) = E(R+p*GCD(m,2*n)/ (2*n*m)).

Other Structures

Force cancellation by the judicious use of symmetry is one of the fundamental principles underlieing the design of molecular bearings. It can also be used in the design of other structures. Roller bearings and planetary gears, to name only two, can also benefit by the appropriate use of symmetry.

Conclusions

We have proven that molecular bearings in which the shaft has m-fold symmetry and the sleeve has n-fold symmetry will, when the bearing is not loaded, have a potential energy which has a period of GCD(m,n)/(m*n). By suitably selecting values for m and n, it is possible to obtain bearings with a short period. In particular, when m and n are relatively prime (e.g., GCD(m,n) equals 1) then the period will be 1/(m*n). Bearings with short periods will usually have small barriers separating one minima from the next, and so the barriers to rotation of the bearing will be small. This conclusion is supported by computer modeling.

The theorem proved here applies to any shaft and sleeve which obey the symmetry conditions. A very wide range of molecular structures which exhibit suitable symmetry can be used. Thus, it is possible in principle to construct "good" molecular bearings from a very wide range of materials by paying attention to the symmetries of the shaft and sleeve.

References
This page is part of the nanotechnology web site.