A Frequently Asked Question: how can we make large, atomically precise products? How can every atom in a large object be perfectly positioned? Doesn't that violate the laws of thermodynamics, or cost huge amounts of energy, or take vast amounts of time, or something?
The answer is no. Which is not all that odd, as rather precise biological molecular machines already exist. Any strong argument against atomically precise molecular machines would also be an argument against the protein-based molecular machines in our bodies which are keeping us alive.
If we really had a strong argument against their feasibility, we might disappear in a puff of logic.
In an imperfect universe errors are going to exist. The largest errors that we can't control are from background radiation. At roughly 3 mSv (millisieverts) per year (0.3 rads per year), background radiation limits us to molecular machines with no more than ten billion atoms if we want an MTBF (Mean Time Between Failures) of 10 years (Nanosystems, page 155). As all other sources of errors (thermal, photochemical, quantum, etc.) can be reduced below this level by proper design and manufacturing methods, it follows that molecular manufacturing can make atomically precise modules with up to ten billion atoms.
Larger structures, those with trillions of atoms and more, must be built from multiple smaller atomically precise modules. Each such module must be testable and replaceable if we find a single defect of any kind. This is a design rule that could easily be followed for molecular computers. Molecular computer modules with ten billion atoms would have more than enough functionality to encompass complete self-diagnostic capabilities, and such modules would be able to interface with other such modules in a redundant network that would continue to function despite failures in multiple modules. Other types of large molecular machines (machines that weren't computers) could likewise be composed of replaceable modules, with a wide range of strategies available for testing and replacing failed modules to ensure continued operation of the larger system.
Alternatively, modules could be designed to continue operating in the face of multiple failures. This would be most easily true for simple structural modules. A diamond strut made of ten billion carbon atoms would suffer little degradation in its load bearing capabilities if a carbon atom, or even dozens of carbon atoms, were knocked out of place. Only if it were stressed to its absolute limit, without the slightest margin for error, would there be any possibility of seeing any change in its actual performance. A molecular machine with ten billion atoms could be designed to be redundant, it just might make the design somewhat more complex. Today, we are avoiding design complexity because we want to make it obvious that the design works, because the resources we have available for the design process are limited, and because our current design abilities are modest. In the future, these contraints will no longer be present. We'll have much more computational capacity and better design software, and will embrace design complexity if it will give us better performance.
The third law of thermodynamics states that the entropy of a perfect crystal at absolute zero, or 0 kelvin is zero (see Wikipedia). Molecular machines will have somewhat higher entropy, even at absolute zero, and their entropy will be further increased because of their operating temperature. Still, molecular machines will have a very low entropy, comparable to that of a single crystal of silicon. Today's semiconductor industry can make remarkably low-entropy defect-free single-crystal silicon, so entropic considerations would seem to pose no bar to making molecular machines of similar (very low) entropy.
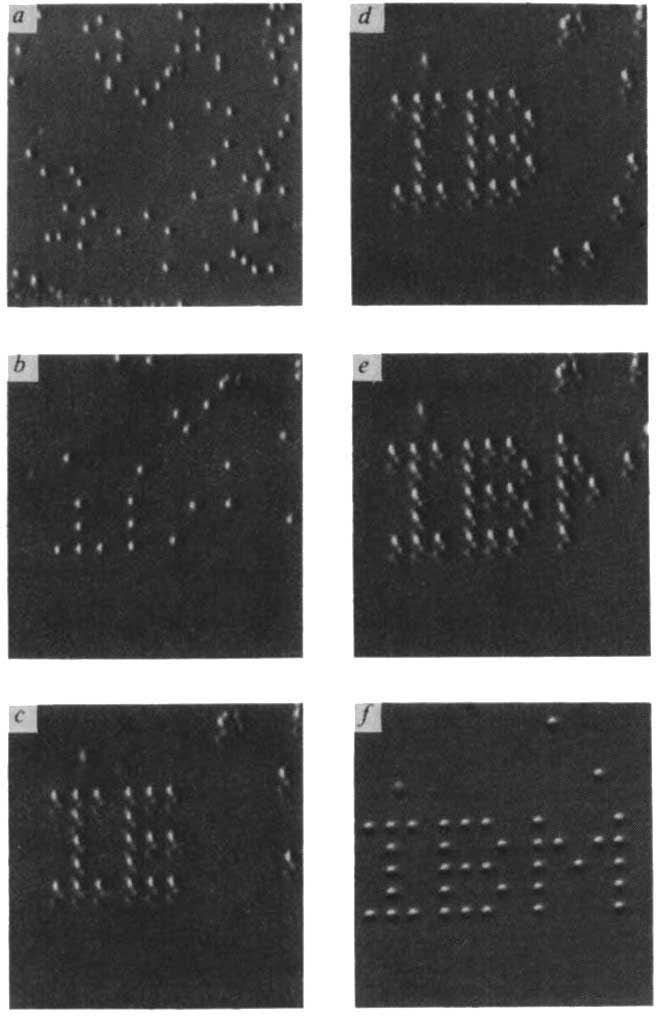
More strongly, the defects in single-crystal silicon arise from the "freezing in" of high-temperature defects that have insufficient time to anneal out when the crystal cools. During mechanosynthesis we will be able to inspect and correct defects. We could, in principle, if there were no processes that were generating defects (which, unfortunately, there are: remember radiation damage), manufacture atomically precise structures of arbitrary size. An example of this would be the process by which the letters "IBM" were formed by Eigler and Schweizer (Nature 344, 524 - 526 (05 April 1990); doi:10.1038/344524a0), even though the process by which they were formed was so error prone that no single pixel could be made without repeated mistakes. The only way the defect-free letters IBM were made was by repeated cycles of inspection and correction, until, eventually, the final structure was achieved.
The fundamental
equation relating thermal noise to positional uncertainty is:
σ2 = kT / ks
(Nanosystems, equation 5.4). This equation relates the positional uncertainty σ to Boltzmann’s constant k, the absolute temperature T and the stiffness ks (usually in Newtons/meter).
Inspection of this equation shows that thermal noise can be
controlled by either or both of two approaches:
decreasing the temperature T or increasing the stiffness ks.
Numerical evaluation of this equation shows
that positional uncertainty of less than an atomic diameter can be achieved at
room temperature when appropriate attention is paid to the stiffness of the
design. Small (~100
nanometer) robotic arms able to accurately position highly reactive molecular
tools in the face of thermal noise at room temperature are feasible, and the reliability improves exponentially as we decrease temperature.
The equation describing the quantum mechanically induced positional uncertainty in the ground state (that is, the positional uncertainty in the limit of low temperature, when thermal noise has no effect) is:
σ2 = ℏ / 2 sqrt(m ks)
where ℏ is Planck’s constant ℎ divided by 2 π, m is the mass, and ks is again the restoring force or spring constant. Numerical evaluation of this equation again shows that molecular machines are feasible, the primary limitation being the ability of hydrogen to tunnel in some situations that are relevant. This limitation can be overcome by designing systems in which the potential destinations to which hydrogen might tunnel are all uphill (for example, the hydrogens are all stably bonded, and tunneling would effectively break a bond). Of greater concern is stability during the mechanosynthetic process, as transient radical sites are created which can provide opportunities for hydrogen migration on intermediate structures. This can be a significant limitation requiring careful analysis of possible tunneling pathways when mechanosynthetic sequences are being designed. However, as multiple mechanosynthetic pathways are available, this is a constraint and not a fundamental limitation.
Nuclei with larger masses (C, N, O, etc.) are less prone to tunneling, sufficiently so that this is not an issue of significant concern except in very special situations.
The simplest answer to photochemical damage is to keep the system in the dark. Even relatively thin layers of shielding are effective. Nanosystems (page 154) concluded that a 250 nm thickness of Al would reduce photochemically induced errors to less than one per 30 years per square micron of direct-sunlight exposed surface.
Mechanosynthesis, the process of manufacturing atomically precise structures, will itself have errors. Any error in this manufacturing process could, if unchecked, result in errors in the final product. At the simplest level, we can characterize the mechanosynthetic manufacturing process (and many other manufacturing processes) by some error rate ε per "basic cycle" or per "step". An error rate of ε means it will be possible to build error free parts that have fewer than 1/ε steps in their manufacture, because our probability of success is good enough that we can keep trying until we succeed. In our case, 1 step adds ~1 atom, so we can build error free parts (a.k.a. atomically precise parts) with 1/ε atoms. If necessary, we can drive down the error rate by adding additional testing in the basic cycle. That is, following each mechanosynthetic step, or following a few steps, we could test to verify that the step or steps came to a satisfactory conclusion. Failure of the test would result in a corrective action. The simplest corrective action would be to reject the entire atomically precise module under construction.While this would slow down the manufacturing process, it would also reduce the error rate. This would be analogous to proofreading in biological systems, which can take place while replicating DNA, transcribing DNA to mRNA, or translating mRNA to proteins.
The finished part is then inspected, and rejected if flawed. Flawless parts are used directly, or to make yet larger parts. Such higher-level manufacturing processes will themselves have some error rate, and we can now apply the previous logic to build larger atomically precise parts from smaller atomically precise parts, these larger parts being of size (1/ε)2. This process can be repeated to build larger and larger atomically precise parts, until we encounter other limits.
Mechanosynthesis uses positional devices: robotic arms. These robotic arms are the first level in a hierarchy of robotic arms of increasing size, the larger arms designed to handle larger parts. This kind of hierarchy can be arranged in an orderly fashion, as in convergent assembly, and parts inspection and rejection of flawed parts can be integrated into the system and take place both immediately upon completion of parts fabrication by mechanosynthesis, and also upon completion of higher-level parts assembly, ensuring that parts at all levels are error free before they proceed into assembly operations at the next higher level. Convergent assembly also provides a general and orderly framework for massive parallelism, so that the simultaneous mechanosynthesis and assembly of parts of all sizes can take place, providing for the rapid assembly of a large finished product. Analysis of the convergent assembly process shows that a mature system could produce finished meter-scale products from nanometer-scale molecular feedstock molecules in a matter of minutes.
Molecular manufacturing will eventually achieve very low error rates in the manufacturing process and in the final product. The anticipated limiting factor is likely to be radiation damage, which sets a limit of ~ten billion atoms to the size of atomically precise modules with an MTBF (Mean Time Between Failures) of ~ten years. Larger atomically precise modules could be used, but their useful lifetime would be shortened.
After atomically precise modules are manufactured, they would be inspected for defects. Defective modules would be rejected, and perfect modules would be accepted for use in subsequent manufacturing steps. This strategy keeps quality high despite a finite rate of module failure. Continued inspection and replacement of modules during their useful lifetimes keeps the overall system operating indefinitely. Provided the overall system is tolerant of some modest percentage of failed modules, and can continue functioning despite their presence, and provided that inspection and replacement of failed modules is carried out at a pace that exceeds the rate at which modules fail, then the probability of overall system failure can be made exponentially small.
Wikipedia says:
The gray - quantity "D": 1 Gy = 1 joule/kilogram - a physical quantity. 1 Gy is the deposit of a joule of radiation energy in a kg of matter or tissue.
The sievert - quantity "H": 1 Sv = 1 joule/kilogram - a biological effect. 1 Sv represents the equivalent biological effect of the deposit of a joule of radiation energy in a kg of tissue. The equivalence to absorbed dose is denoted by Q. The conversion is 1 millisievert = 0.1 rads.
As we're discussing damage done to molecular machines, which we expect will be largely diamondoid, there is no appropriate unit that has exactly the value that we want. However, the actual level of damage done by radiation to a molecular machine should be accurately represented by something between a Gy and a Sv.
MIT News says:
Basic conversions:
1 gray (Gy) = 100 rad
1 rad = 10 milligray (mGy)
1 sievert (Sv) = 1,000 millisieverts (mSv) = 1,000,000 microsieverts (μSv)
1 sievert = 100 rem
1 becquerel (Bq) = 1 count per second (cps)
1 curie = 37,000,000,000 becquerel = 37 Gigabecquerels (GBq)
For x-rays and gamma rays, 1 rad = 1 rem = 10 mSv
For neutrons, 1 rad = 5 to 20 rem (depending on energy level) = 50-200 mSv
For alpha radiation (helium-4 nuclei), 1 rad = 20 rem = 200 mSv
This is part of Ralph C. Merkle's nanotechnology web site. It can be found on the web at http://www.zyvex.com/nano.