Abstract

One of the fundamental requirements for positional assembly of molecular machines is the availability of molecular parts. One class of molecular parts might be characterized as molecular building blocks, or MBBs. With an atom count ranging anywhere from ten to ten thousand (and even more), such MBBs would be synthesized and positioned using existing (or soon to be developed) methods. Thus, in contrast to investigations of the longer term possibilities of molecular manufacturing (which often rely on mechanisms and systems that are likely to take many years or even decades to develop), investigations of MBBs focus on nearer term developmental pathways.

Introduction

A more attractive approach as a target for near term experimental efforts is the use of molecular building blocks (MBBs) (Krummenacker, 1992; Merkle, 1999). Such building blocks would be made from dozens to thousands of atoms (or more). Such relatively large building blocks would reduce the positional accuracy required for their assembly. Linking groups less promiscuous than the radicals proposed for the synthesis of diamond would also reduce the rate of incorrect side reactions in the presence of contaminants. Because this approach uses positional assembly at the molecular scale, and because positional assembly of molecules was, until recently, not a possibility that had been considered seriously, there has been remarkably little research in this area. As a consequence, the present paper will concentrate on providing perspective on the possibilities, along with a few examples to elucidate the more general principles. Further research into MBBs should prove well worth the effort.

The proposal to use molecular building blocks raises the obvious question: what do they look like? In this paper we consider a number of ideas and research directions which could be pursued to develop a firmer answer to this question.

Polymers are made from monomers, and each monomer reacts with two other monomers to form a linear chain. Synthetic polymers include nylon, dacron, and a host of others. Natural polymers include proteins and RNA (Watson et al., 1987) which, if the sequence of monomers forming the polymer is selected carefully, will fold into desired three dimensional shapes. While it is possible to make structures this way (as evidenced by the remarkable range of proteins found in biological systems), it is not the most intuitive approach (the protein folding problem is notoriously difficult).

A second drawback of this approach is the relative lack of stiffness of the resulting structure. The correct three dimensional shape is usually formed when many weak bonds combine to give the desired conformation greater stability and lower energy than the alternatives. However, this desired structure can usually be disrupted by changes in temperature, pressure, solvent, dissolved ions, or relatively modest mechanical force.

These limitations, caused in large measure by the restriction to two linking groups per monomer, motivates our investigation of MBBs with three or more linking groups.

An excellent review of well characterized linear rigid-rod oligomers formed by a variety of methods (Schwab et al., 1999) provides examples of the best exceptions to the general rule that polymers are floppy, though even here the rigidity is variable. However, giant molecules or supramolecular assemblies composed from the shorter and stiffer rods, particularly if well cross braced, might well prove to be extremely useful in the synthesis of stiff three dimensional structures.

The virtues of positional assembly, strength and stiffness

There are two ways to assemble parts: self assembly and positional assembly. Self assembly is widely used at the molecular scale, and we find many examples of its use in biology (Watson, 1987). Positional assembly is widely used at the size scale of humans, and we find many examples of its use in manufacturing. Our inability to use positional assembly at the molecular scale with the same flexibility that we use it at the human scale seriously limits the range of structures that we can make.

By way of example, suppose we tried to make radios using self assembly. We would take the parts of the radio and put them into a bag, shake the bag, and pull out an assembled radio. This is a hard way to make a radio and if we demanded that all manufacturing take place using this approach our modern civilization would not exist.

By the same token, the range of things that can be made if we restrict ourselves to self assembly is much smaller than the range of things that can be made if we permit ourselves to add positional assembly to the other methods at our disposal. That this rather obvious point has not been more rapidly and generally understood with respect to the synthesis of molecular scale objects stems from the fact that we have never before been able to do positional assembly at the molecular scale. The idea of making a molecular structure by positionally assembling molecular parts is unfamiliar and different. Yet this capability, which has been demonstrated in nascent form by experimental work using the SPM (Scanning Probe Microscope) (Jung et al., 1996; Drexler et al., 1991, chapter 4 for a basic introduction) is clearly going to revolutionize our ability to make molecular structures and molecular machines (Drexler, 1992; Feynman, 1960).

Positional assembly is done using positional devices. At the scale of human beings, the major problem in positional assembly is overcoming gravity. Parts will fall down in a heap unless they are held in place by some strong positional device. At the molecular scale, the major problem in positional assembly is overcoming thermal noise. Parts will wiggle and jiggle out of position unless they are held in place by some stiff positional device (Merkle, 1999).

The fundamental equation relating positional uncertainty, temperature and stiffness is:

s² = k_bT/k_s

Where s is the mean error in position, k_b is Boltzmann's constant, T is the temperature in Kelvins, and k_s is the "spring constant" of the restoring force (Drexler, 1992). If k_s is 10 N/m, the positional uncertainty s at room temperature is ~0.02 nm (nanometers). This is accurate enough to permit alignment of molecular parts to within a fraction of an atomic diameter.

A stiffness of 10 N/m is readily achievable with existing SPMs, but stiffness scales adversely with size. As we shrink a robotic arm, it gets less and less stiff and more and more compliant, and less and less able to position a part accurately in the face of thermal noise. To keep it stiff we have to make it from stiff parts. This is the fundamental driving force behind our desire to keep the MBB stiff.

In summary: stiffness is a fundamental design objective because we want to use positional assembly on molecular parts despite the positional uncertainty caused by thermal noise. This objective permeates our MBB design considerations.

The advantages and characteristics of molecular building blocks

• Larger size. This means lower precision positional devices can satisfactorily manipulate the MBB.
• More links between MBBs. As discussed in the next section, more linking groups on each building block implies more links between building blocks, greater stiffness (better bracing) and greater ease in forming three dimensional structures.
• Greater tolerance of contaminants. Larger building blocks can have greater interfacial area, thus permitting the use of multiple weak bonds between building blocks (instead of fewer stronger bonds). As the particular pattern of interfacial weak bonds can be quite specific, two building blocks will bind strongly to each other while other molecules will bind weakly if at all. This principle, taken directly from self-assembly, is of great help in improving the ability of MBBs to tolerate dirt and other contaminants. This specificity also improves the ability of the MBBs to link even when positional accuracy is poor.
• More accessible experimentally. While theoretical proposals clearly show the great potential of positional control when applied to very small building blocks (and even, under appropriate circumstances, individual atoms), the requirement for high precision and the intolerance of contaminants makes these proposals experimentally inaccessible with existing capabilities. MBBs can be relatively easy to synthesize and more tolerant of positional uncertainty and contaminants during assembly.
• Ease of synthesis. Experimentally accessible MBBs must be synthesizable. As lower-strain structures are easier to synthesize, and polycyclic structures provide greater strength and stiffness, very low strain polycyclic structures (as in, e.g., diamond or graphite) are likely to be common in good MBBs. An exception to this general rule might be the construction of deliberately strained MBBs to facilitate the construction of curved surfaces (which would otherwise create strain in the inter-building-block linking groups) and to stabilize the cores of dislocations.
• A larger design space. Perhaps the greatest advantage of MBBs is their vast number. As we increase their size the number of possible MBBs increases exponentially, giving us a combinatorially larger space of possibilities from which to select those few MBBs that best satisfy our requirements. While making it easier to satisfy our primary design constraints (ease of synthesis, number and specificity of inter-building-block linking groups, etc), this also makes it easier to satisfy secondary objectives such as non-flammability, non-toxicity, an existing literature, ability to work in multiple solvents as well as vacuum, tolerance of higher temperatures, etc.

Following the discussion of MBBs and how to link them, we discuss higher-level strategies for making structures from them. The most obvious distinction is between subtractive synthesis (removing MBBs you don't want from a larger crystal) and additive synthesis (adding MBBs you want to a smaller workpiece). The use of these two approaches places somewhat different requirements on the MBBs.

The goal of making larger MBBs might also be achieved by making them from smaller MBBs. The section on "starburst crystals" discusses an approach to this which might permit the synthesis of very large MBBs (perhaps ten nanometers or larger).

Finally, we consider what we might want to make from MBBs. If our objective is to implement positional assembly, then the most obvious thing to build is some sort of positional device. Other target structures, less ambitious than a complete positional device but which would be of use in a positional device, might be synthesized sooner as part of a longer term program.

Linking groups

MBBs with three linking groups readily form planar structures because three points define a plane. Graphite, formed from sp² carbon atoms which bond to three adjacent neighbors, is a planar structure that is quite strong and stiff in two dimensions but which, like paper, is readily folded through a third dimension. Just as paper can be formed into tubes to improve its stiffness, so can graphite be formed into tubes (often called bucky tubes).

MBBs with three linking groups could, like sp² carbon, form planar structures with good in-plane strength and stiffness, but would be weak and compliant in the third dimension. While this problem could be reduced by forming tubular structures, stiff structures made using this approach would have to be made from many MBBs, as small numbers of MBBs (too few to form tubular structures) would lack stiffness.

MBBs with four linking groups not in a common plane are convenient for building three dimensional structures (much as the four bonds in a tetrahedral sp³ carbon atom allow it to form a stiff, polycyclic three-dimensional diamond lattice).

MBBs with three linking groups can be paired, each member of the pair sacrificing one linking group to form the pair. The pair of MBBs effectively has four linking groups (two available linking groups being provided by each member of the pair). Particularly if the four resulting linking groups are non-planar, the pair can be viewed as a single MBB with four linking groups. In this somewhat roundabout fashion, MBBs with three linking groups can form three dimensional structures much as MBBs with four linking groups.

MBBs with five linking groups can form three dimensional solids. For example, an MBB might have three in-plane linkage groups with inter-linkage-group angles of 120°; and have two out-of-plane linkage groups, both of which are normal to the plane (one linkage group pointing straight up, the other straight down). Such an MBB could form hexagonal sheets by using the three in-plane linkage groups, (each MBB corresponding to a single carbon atom in a sheet of graphite) but would also be able to link together adjacent sheets by using the two out-of-plane linking groups. The unit cell would have hexagonal symmetry.

MBBs with six linking groups can be connected together in a cubic structure, the six linking groups corresponding to the six sides of a cube or rhombohedron. MBBs with six linkage groups can naturally and easily form solid three dimensional structures in the same fashion that cubes or rhomboids can be stacked.

Buckyballs (C₆₀) have now been functionalized with six functional groups (Hutchison et al., 1999; Quin and Rubin, 1999), opening up the possibility of using them as molecular building blocks for the construction of three dimensional structures.

An MBB with six in-plane linkage groups can form a particularly strong planar structure or sheet. The conformation of the sheet would depend only on the length of the inter-MBB links, and not on any ability of the MBB to maintain two linkage groups at some specific angle. As the distance between linked MBBs can often be controlled more effectively (the stretching stiffness of the link can be higher) than the angle between adjacent linkage groups (the bending stiffness is usually lower), this structure can be significantly stiffer in-plane than a planar structure formed from similar MBBs with three linkage groups.

Cubic or hexagonal close packed crystal structures are very stiff, involving 12 linking groups from each MBB. These structures can be described as follows: two very stiff sheets (six linkage groups in-plane) can be laid on top of each other. Each MBB in the upper sheet can be linked to three MBBs in the lower sheet (which form the vertices of a triangle). This arrangement can be repeated with a third, fourth, and more sheets. Six linkage groups connect each MBB to six in-plane neighbors, three linkage groups connect each MBB to three MBBs from the plane below, and three linkage groups connect each MBB to three MBBs from the plane above. The major advantage of this type of MBB is that the stiffness of the whole structure depends only on the stretching stiffness of the links between MBBs and not on the angular stiffness between adjacent linkage groups. This can be useful when the angular stiffness is poor, but the stretching stiffness is good.

MBBs with four linking groups can be paired, each member of the pair sacrificing one linking group to form the pair. The pair of MBBs effectively has six linking groups (three available linking groups being provided by each member of the pair). The pair can be viewed as a single MBB with six linking groups. This again leads naturally to unit cells that are cubic or rhomboid, but with each unit cell comprising two MBBs. This is similar to the primitive unit cell of diamond, which has two carbon atoms.

In summary, MBBs with two linking groups form three dimensional structures only with difficulty and only by using indirect and complex methods. MBBs with three linking groups readily form planar structures, which are strong and stiff in the plane but bend easily, like a sheet of paper, unless rolled into tubular structures to improve stiffness. They can also be used (although somewhat less naturally) to directly form three dimensional solids with a unit cell having four MBBs. MBBs with four linking groups quite naturally form strong, stiff three dimensional solids in which the unit cell is composed of two MBBs (as in diamond). MBBs with five linking groups can readily form strong, stiff three dimensional solids in which the unit cell is composed of six MBBs. MBBs with six linking groups readily form strong, stiff three dimensional solids in which the unit cell is composed of a single MBB. They can also form very stiff sheets if all linkage groups are in-plane, though this arrangement sacrifices stiffness out-of-plane. MBBs with twelve linking groups can form very strong and stiff three dimensional solids.

While MBBs can have any number of linkage groups, MBBs with fewer linkage groups are usually (though not always) more readily synthesized. If we seek an MBB with the least number of linkage groups that can still readily form strong, stiff three dimensional structures, then MBBs with four linkage groups are quite attractive. A high symmetry structure with four linkage groups will have tetrahedral symmetry (with an inter-linkage-group angle of approximately 109°). Much of the discussion in this paper is about specific tetrahedral MBBs.

Self assembled versus positionally assembled MBBs

In contrast, MBBs for positional assembly need not be soluble and do not even need a solvent: they can be used in vacuum. Like bricks, they can be picked up and moved to the desired location whether they are soluble or not.

If two MBBs can bond strongly to each other in two or more different configurations, then the self assembly process will randomly select from among these multiple configurations and produce a random clump of MBBs rather than any specific desired arrangement. For this reason, MBBs for self assembly often use multiple weak bonds, rather than a few strong bonds. Any particular weak bond can be broken by thermal noise. Only when the action of multiple weak bonds is combined does the resulting configuration of MBBs remain stable. Configurations that simultaneously enable multiple weak bonds are relatively rare, and so it is easier to design MBBs with multiple weak bonds that self assemble into a single desired structure.

While the use of strong bonds in self assembly is possible, positional assembly can more readily use MBBs that form a few very strong bonds. Inappropriate interactions between positionally assembled MBBs are prevented by the simple expedient of keeping them away from each other. When two MBBs are brought together, their orientations are controlled to prevent inappropriate bond formation. Thus, selective control over bond formation is achieved through positional control, rather than by designing the MBBs to be selective in bond formation. This approach permits the use of highly reactive MBBs that would be entirely inappropriate for self assembly.

The disadvantage of highly reactive MBBs is that they must be positionally controlled at all times. They cannot be allowed to mix randomly at any time, as this would cause them to rapidly form unusable clumps. While achievable, this imposes a number of constraints that are more difficult to meet with today's systems.

An alternative approach is to use protecting groups that cover or alter the highly reactive linkage groups. These protecting groups would then be removed when two positionally assembled MBBs were joined. The use of protecting groups is common in chemical synthesis, though the concept of selectively removing a protecting group from a single molecule by using positional control is still novel. Selective photoactivation of molecules within a region comparable in size to the wavelength of light is well known and used commercially. From the perspective of nanotechnology, regions that are hundreds of nanometers in size are very large, making optical approaches rather imprecise when viewed from the perspective of the desired long term objectives.

Positionally assembled MBBs must be held, while self assembled MBBs need not be held. This implies that positionally assembled MBBs must have "handles" by which they can be gripped. While it is possible in some cases to use the linkage groups of the MBB as handles, these linkage groups might well be intended to irreversibly form strong bonds. Because it is essential in positional assembly both to hold the MBB and to let go, such an MBB must be able to form reversible attachments to the positional device. Ideally, this would be done using a variable affinity binding site which has two states: bound and unbound. The tip of the positional device first binds to the MBB. Then it positions the MBB with respect to some workpiece under construction, to which the MBB bonds. Finally, the positional device releases the MBB. Tweezers serve this function: when closed they can grasp an object (high affinity), when open they release the object (low affinity). While there are many other designs for variable affinity binding sites (Merkle, 1997b), tweezers are widely applicable and illustrate the basic concept.

Pragmatically, the greatest advantage of self assembled MBBs is the extensive literature on self assembly and the extensive set of existing experimental techniques that have been used to self assemble some impressively complex structures. Positional assembly at the molecular scale, by contrast, is still in its infancy. For example, the self assembly of DNA into complex molecular structures has made remarkable strides (Seeman, 1994), and has been used to make a truncated octahedron (Zhang, 1994). To quote Seeman and coworkers (Seeman et al., 1997):

There are several advantages to using DNA for nanotechnological constructions. First, the ability to get sticky ends to associate makes DNA the molecule whose intermolecular interactions are the most readily programmed and reliably predicted: Sophisticated docking experiments needed for other systems reduce in DNA to the simple rules that A pairs with T and G pairs with C. In addition to the specificity of interaction, the local structure of the complex at the interface is also known: Sticky ends associate to form B-DNA. A second advantage of DNA is the availability of arbitrary sequences, due to convenient solid support synthesis. The needs of the biotechnology industry have also led to straightforward chemistry to produce modifications, such as biotin groups, fluorescent labels, and linking functions. The recent advent of parallel synthesis is likely to increase the availability of DNA molecules for nanotechnological purposes. DNA-based computing is another area driving the demand for DNA synthetic capabilities. Third, DNA can be manipulated and modified by a large battery of enzymes, including DNA ligase, restriction endonucleases, kinases and exonucleases. In addition, double helical DNA is a stiff polymer in 1-3 turn lengths, it is a stable molecule, and it has an external code that can be read by proteins and nucleic acids. [references omitted from this quote]

Abstract properties of tetrahedral MBBs

First and foremost, the linkage groups will have particular properties. Of crucial concern are the conditions under which the links are made, and the extent to which inappropriate links are possible. If a specific functional group, call it R, bonds readily with other functional groups of type R (as is true for radicals), then the MBB cannot be kept in solution without rapidly forming undesired clumps. These limitations can be overcome by the use of protecting groups (or otherwise introducing some barrier to reaction) although this adds the additional requirement that the protecting groups be removed before an MBB is added to a growing workpiece.

A second type of linkage will involve two distinct functional groups, call them A and B. Functional groups of type A will readily bond with functional groups of type B, but A will not bond to A and B will not bond to B. The Diels-Alder reaction (Krummenacker, 1994) is a good illustration of this kind of functional group. The diene and dieneophile (corresponding to functional groups of type A and type B) will bond to each other, but not to themselves. They also bond to little else, and so can be used in most solvents (or in vacuum) and in the presence of impurities. As there are no leaving groups, the reaction itself does not introduce any possibly undesired contaminants.

A second advantage of the A-B functional groups is their increased tolerance of positional uncertainty. Consider two types of MBBs, type A and type B. Type A MBBs have four linkage groups of type A, while type B MBBs have four linkage groups of type B. Type As cannot link with other type As, nor can type Bs link with other type Bs. When type A and type Bs are combined in the diamond (or actually zinc-blende or wurtzite (hexagonal)) crystal lattice, they alternate. Each A is surrounded by four Bs, and each B is surrounded by four As.

In both the zinc-blende and wurtzite structures, there are no cycles of length five but many cycles of length six. That is, if we traverse a path from one MBB to another along the links between them, we will never find that we have completed a cycle and returned to the starting MBB without including at least six MBBs along the path. Clearly, a cycle with an odd length (such as five) would imply that either two As were linked or that two Bs were linked. This is forbidden by the nature of the A-B building blocks.

If, however, we were using MBBs of type R, which can readily link to each other, than a path of length five would be possible if the geometry of the MBBs was sufficiently distorted. Such a distortion might occur if the linking groups were insufficiently stiff, and permitted Rs near the edge of the crystal to come into contact with each other. This is exactly what happens on the diamond (100) surface, which forms strained dimers from adjacent carbon atoms which, if they were part of the bulk, would be separated by an additional carbon atom between them.

The use of A-B MBBs eliminates the possibility of odd cycles, and particularly cycles of length five. However, it does not eliminate cycles of length four, which could in principle occur if the geometry were sufficiently strained. As the strain required to achieve a cycle of length four is greater than the strain required to achieve a cycle of length five, R MBBs in a diamond lattice will more readily produce undesired cycles of length five than similar A-B MBBs will produce undesired cycles of length four.

This principle can be extended by introducing more types of functional groups, D, E, F, .... The more types of functional groups, the more strained the geometry must be before an incorrect link can be formed. In the limit, an arbitrary finite structure composed of a fixed number of MBBs arrayed in a regular lattice similar to diamond (or related structures) would have functional groups all of which were distinct and unique. Self assembly of such a structure would occur when the MBBs were mixed, and positional assembly would not be required at all. One method of providing a very large number of distinct types of functional groups is with DNA. There are many short DNA sequences that are selectively sticky, and which would bond only to the appropriate complementary sequence. Experimental work linking gold nanoparticles with DNA suggests this approach is experimentally accessible (Mirkin, 1996).

This illustrates a more general point: self assembly and positional assembly are endpoints on a continuum. As positional accuracy becomes poorer and poorer, "positional" assembly becomes more like self assembly. The techniques used in self assembly to ensure accurate assembly despite positional uncertainty can be gradually introduced into positional assembly as accuracy degrades.

This also illustrates the importance of stiffness in the linkage groups. The stiffer the linkage groups, the less likely that links will be formed where they shouldn't be. In the limit, sufficiently stiff linkage groups would entirely prevent incorrect structures from forming. Provided the linkage groups have an appropriate orientation, the resulting structures will be unstrained (e.g., tetrahedral sp³ carbon atoms form unstrained bonds in diamond).

Proposals for MBBs

MBBs should be stiff, strong, and synthesizable with existing methods. Stiffness and strength are attributes derived from many strong bonds. Polycyclic molecules are usually stronger and stiffer than molecules without cycles (linear or tree structured molecules). Unstrained structures are usually easier to synthesize than strained structures. A good MBB is therefore likely to be polycyclic, with many strong, almost unstrained bonds. Given that bond-bond angles are often 120° (trigonal) or 109° (tetrahedral), we are likely to see hexagonal planar structures (as in graphite), or diamond and related structures. It should therefore come as no surprise that MBBs that resemble bits of graphite with appropriately functionalized edges, or bits of diamond with appropriately functionalized surfaces, are good candidates for MBBs. The diamond lattice in particular can be modified by substitution of carbon by elements from column IV: silicon, germanium, tin, or lead. Edge or surface atoms on the MBB can be chosen from columns III, V or VI, as appropriate (or alternatively the surface atoms can simply be hydrogenated).

Adamantane (hydrogens omitted for clarity)

1,3,5,7-tetraaza-adamantane (methenamine) (hydrogens omitted for clarity)

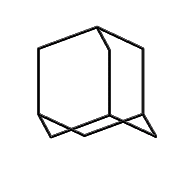
This line of reasoning leads fairly directly to molecules like adamantane: a stiff tetrahedral molecule which can incorporate heteroatoms and can be readily functionalized. Composed of 10 carbon atoms the Beilstein database (see www.beilstein.com) lists over 20,000 variants, supporting the idea that this family of molecular structures is large, contains many readily synthesized members, and has enough "design space" to provide solutions able to satisfy the multiple constraints imposed on a "good" molecular building block. This conclusion is further supported by (Fort, 1976), who surveyed adamantane chemistry.

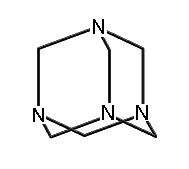
A few molecules in this class which have been synthesized include adamantane; 1,3,5,7-tetrasila-adamantane; 1,3,5,7 tetrabora-adamantane (not yet synthesized, though 1-bora-adamantane has been synthesized); 1,3,5,7-tetraaza-adamantane (more commonly known as methenamine, readily synthesized and with a variety of commercial applications (Budavari et al., 1996)); 2,4,6,8,9,10-hexamethyl-2,4,6,8,9,10-hexabora-adamantane; and many others.

Tetramantane (hydrogens omitted for clarity)

Larger bits of diamond that have been synthesized include diamantane (C₁₄H₂₀), triamantane (C₁₈H₂₄), and even tetramantane (C₂₂H₂₈). Pentamantanes (C₂₆H₃₂) and hexamantanes (C₃₀H₃₆) occur naturally in some deep gas deposits (Schoell and Carlson, 1999; Dahl et al., 1999) but are not readily accessible in the laboratory.

Other small stiff structures that might be used as the basis for building blocks include cyclophanes, iceanes (small pieces of "hexagonal diamond,"), buckyballs, buckytubes, alpha helical proteins (Drexler, 1994), and a host of others.

An aside on "bond strength"

In common (non-chemical) usage, "strength" refers to a maximum force, not an energy. Energy and strength are not the same, as the Newtonian equation relating work and force is Work = Force times Distance. Knowing the energy does not tell us the force that must be applied unless we also know the distance over which that force must work. In chemistry, a reasonable approximation to the stretching potential between two bonded atoms is the Morse potential:

U(x) = D_e[1 - e^-b(x-r₀)]²

Where U(x) is the potential energy of the system as a function of the separation x between the two bonded atoms, D_e is the "bond strength" as an energy, e is 2.71828..., r₀ is the equilibrium distance (minimum energy distance), and b is a parameter which, along with D_e, determines the stiffness k_s of the bond. As k_s is readily determined from the vibrational frequency and the mass of the vibrating atoms, and D_e (with some adjustment for the zero point vibrational energy) is determined from chemical data about the bond strength, the parameter b can then be determined using the formula (Drexler, 1992):

b = sqrt(k_s/ (2 D_e))

If we pull on the bond with a large enough steady force, it will eventually break. This occurs at a force of b D_e / 2. Using these equations, and knowing vibrational frequencies, atomic mass, and "bond strength" as an energy, we can compute the actual force required to break a bond. The force required to break a single carbon-carbon bond is ~6 nanonewtons. As the "strength" of the dipolar bond measured as an energy is almost one order of magnitude less, and the stiffness is not substantially less, we would expect that a force of roughly 1 nanonewton would be sufficient to break a dipolar bond.

The use of energies to measure bond strengths is appropriate if we expect that thermal noise is the disruptive force that will break bonds. The time until a bond is thermally disrupted is given by: t_break = t₀ e^D_e/k_bT

where k_b is Boltzmann's constant, T is the temperature in Kelvins, and t₀ is a constant characteristic of the particular system (on the order of 10^-13 for "typical" bonds). As can be seen, bonds with an energy "strength" significantly in excess of thermal noise will not be disrupted by thermal noise for a very long time.

Possible linking groups

How might we link adamantane-based MBBs? (hydrogens omitted for clarity)

How, then, might we link together two adamantane-based MBBs? One possibility which illustrates the concept is the use of dipolar bonds between nitrogen and boron. This is motivated less from any existing common polymer than from the observation that the simplest, stiffest and most direct method of linking two MBBs is to form a bond between two atoms, one atom from each adamantane. While radicals could be used, they suffer from certain drawbacks (clumping during synthesis, for example). The dipolar bond, on the other hand, permits synthesis of the B and N MBBs separately. While much stronger than hydrogen bonds, dipolar bonds are weaker than normal covalent bonds. Their strength can vary substantially, generally in a range from ten to a few tens of kcal/mol.

A central 1,3,5,7 tetrabora-adamantane MBB linked to four surrounding 1,3,5,7-tetraaza-adamantane MBBs.

If we use 1,3,5,7 tetrabora-adamantane and 1,3,5,7-tetraaza-adamantane as "B" and "N" building blocks, then each linking atom (N or B) is bonded to three other atoms in its MBB, thus providing a stiff support. The class of structures that can be formed includes the kind of structures typical of (for example) silicon carbide, where alternating silicon and carbon atoms are each bonded to four neighboring atoms of the other type. The B and N type adamantane-based MBBs are, in essence, larger versions of the same concept.

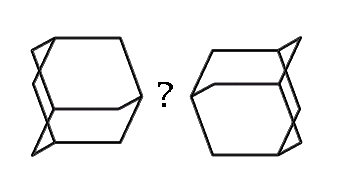
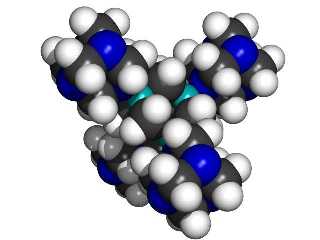
While 1,3,5,7 tetrabora-adamantane has not been synthesized, DFT calculations using a 6-311+G(2d,p) basis set show the molecule is a minima on the potential energy surface (Halls, 1999, private communication). Further, DFT calculations using a somewhat smaller 6-31G(d) basis set show that a dimer composed of an N and a B building block connected by a dipolar bond is also a minima on the potential energy surface with an enthalpy of formation of about 20 kcal/mol (ZPE corrected) (Halls, 1999). While boron with three single bonds is normally planar, it is strained by the tetrahedral nature of the adamantane cage. Stabilization of the boron atoms in the tetrahedral (rather than planar) bonding pattern by suitable electron donor groups (e.g., NH₃) should increase the stability of the building-block plus four-donor-groups complex.

Hydrogen bonds

Hydrogen bonds are common in biological systems. They are relatively weak, on the order of 2-5 kcal/mol, but involve straightforward and widely practiced chemistry and can provide reasonable strength when several are combined (Watson et al., 1987). Two carboxcylic acids form a dimer via hydrogen bonds to each other with a ΔH of -14.1 to -16.4 kcal/mol in gas phase (Jones, 1952). If we use adamantane 1,3,5,7 tetracarboxylic acid (four COOH groups at the four trigonal carbon atoms of adamantane) as an MBB, each MBB can readily form eight hydrogen bonds to adjacent MBBs in the crystal if we assume that the MBBs are arranged like the carbon atoms in diamond. However, the resulting crystal structure would have large empty spaces. Experimental determination of the crystal structure (Ermer, 1988) shows five interpentetrating diamondoid lattices, thus effectively filling the large voids that a single diamondoid lattice would create.

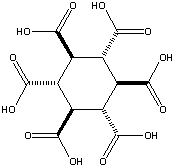
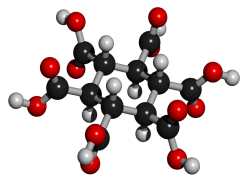
Addendum added January 24, 2002: A theoretical possibility would be cyclohexane-1,3,5/2,4,6-hexacarboxylic acid (see figures at left, the graphic showing the energetically preferred all equatorial isomer). This MBB has six linking groups and each linking group could have two hydrogen bonds. While the all cis isomer -- cyclohexane-1,2,3,4,5,6-hexacarboxylic acid with three axial and three equatorial groups -- has been synthesized and is available commercially, it does not form an obvious crystal structure in which 12 well aligned hydrogen bonds can form. By contrast, while cyclohexane-1,3,5/2,4,6-hexacarboxylic acid has not been synthesized there is a theoretical crystal structure which forms 12 well aligned hydrogen bonds and has no large voids. Seven such MBB's arranged in the appropriate structure are shown in the following figure:

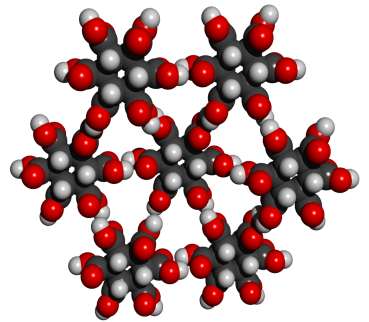
Whether or not this theoretical crystal structure would actually form has not been experimentally determined. No obvious alternative structure would permit good alignment of all 12 hydrogen bonds. The pdb file for a cluster with eight MBB's is here. There are many readily imaginable variants that have the same or a similar motif.

Addendum added March 15th 2002: "Acid B [all equatorial cyclohexane hexacarboxylic acid] is formed from acid A [all cis cyclohexane hexacarboxylic acid, commercially available] by heating with hydrochloric acid, ..." (English translation of German patent by Badische Anilin and Soda-Fabrik Aktiengesellschaft, Convention Application No. 2212369, filed March 15 1972).

A paper that sheds tangential light on the possible crystal structure of "Acid B" is "The crystal structure of mellitic acid, (benzene hexacarboxylic acid)" by S.F. Darlow, Acta Cryst. (1961) 14, pages 159-166. This related molecule forms crystal with a structure as one might expect from the discussion here, differing largely in that it forms layers -- a two-dimensional rather than a three-dimensional network of hydrogen bonds.

Tridentate complexes with transition metals

Six linkage groups using adamantane

Making larger building blocks from smaller ones

Using two building blocks that alternate to form a crystal, a somewhat related but more structurally specific process (which we might call starburst crystals) would be to start with a single building block of type A and link it to as many building blocks of type B as possible (typically four or six). This might be done by adding a dilute solution of A to a concentrated solution of B, and then separating the AB_n results, where n corresponds to the number of linkage groups on A, under the assumption that all such linkage groups will be saturated with B building blocks. If the A building block is designated A⁰, then we might call the A building block surrounded by B building blocks A¹.

This process can be repeated, the A¹ building block can be mixed into a concentrated solution of A building blocks, adding an additional layer to the growing crystal and producing A². A² can be mixed into a concentrated solution of B building blocks, producing A³.

The critical difference between this process and the growth of a starburst dendrimer is that starburst crystalization adds building blocks only at those sites which extend the crystal structure. Thus, a new building block added in the Nth layer might bind to two or even three building blocks from layer N-1. Rather than exponential growth in the number of steps, this process has a growth rate that is cubic in the number of steps and the structure that results can be viewed as that part of a crystal that includes all crystal elements within a certain distance from some center.

If a building block added to layer N links to two building blocks from layer N-1, then it must link to the right two building blocks. If the links between building blocks are sufficiently stiff, this is not a problem. The new building block in layer N can only link appropriate pairs of building blocks from layer N-1. However, if the linkages are too floppy, the new building block might link to an incorrect pair of building blocks from layer N-1, producing an incorrect result. Preventing this requires either control over the geometry of growth (the bonds between building blocks cannot be too floppy) or selective control over linkage formation (different chemistries could be used for the formation of different links, even from the same building block; or linkage groups could be protected and de-protected).

Additive and subtractive synthesis

One method of additive synthesis is to add invididual building blocks (rather than groups of building blocks) one at a time. Using positional assembly, this requires a method of grasping and releasing the individual building blocks. As the building blocks already have four sites designed to bind to the complementary building block, these sites could be used to "grip" the building blocks while they were positioned. The tip of the positional device would need to be specifically designed to bind to the building blocks strongly enough to hold them while they were being positioned and oriented, but weakly enough that they could be released when the positional device was withdrawn from the workpiece under construction (or, alternatively, the tip could undergo some change to reduce its binding affinity for the building blocks).

Using substractive synthesis, undesired building blocks could be removed by scraping them away. The major advantage of this approach is that the tip of the positional tool need not bind to the building blocks, and therefore a much wider range of tip structures would be acceptable. Orientation requirements for the tip would also be relaxed. Force applied to a single building block on the surface would break it free from the workpiece. Provided that the bonds holding the building block together were significantly stronger than the bonds between building blocks, whole building blocks would be removed from the workpiece (rather than fragmenting the building blocks).

Subtractive synthesis has another advantage: adding building blocks one by one will on occasion produce situations where the new building block is bound to the workpiece by a single bond (the first building block to be added on a (111) surface, for example). Because it is held by only a single bond, the building block will not be as well bound to the rest of the structure and would have a higher probability of falling off before further building blocks could be added. This is of particular concern when weak bonds are being used between building blocks.

By contrast, substractive synthesis can leave intact all bonds that will be present in the final (desired) structure. If the final structure has been designed so that each building block is held in place by at least two bonds, then at every point during synthesis every building block that will be kept will be held in place by at least two (and often three) bonds. As the probability that a building block will break away from the workpiece is an exponential function of the depth of the potential energy well in which the building block finds itself, and as the depth of this well is doubled when two bonds hold it in place as compared with only a single bond, this difference can be significant.

One of the intriguing aspects of subtractive synthesis is the remarkably wide range of potential building blocks that could be used. Virtually any large, reasonably stiff and reasonably compact organic molecule that remains crystalline at reasonably high temperatures could be used. Adamantane itself, for example, melts at 268°C. (Weast, 1989). Such building blocks would be held together primarily by van der Waals forces, which would increase as the size of the building blocks increased. Precise modification by an SPM in UHV (Ultra High Vacuum) would seem feasible provided the tip was sharp in comparison with the size of the building block. The primary concern would be that building blocks on the surface (rather than in the bulk) might be so weakly bound that they would leave the surface. This could in general be dealt with by lowering the temperature, but a more careful search through the space of possibilities for building blocks that remained bound to the surface at room temperature might prove simpler. It might also be possible to find building blocks that could be selectively removed without the use of UHV, further simplifying the experimental procedure.

What to build?

A second obviously desirable structure would be a joint, which would provide one degree of rotational freedom and essentially no other degrees of freedom. The feasibility of sliding surface joints would depend in large part on the precise nature of the building blocks, but there is in general no problem in designing bearings with sliding surfaces (Merkle, 1993b). If the surfaces are not otherwise attractive to each other (e.g., hydrogen terminated carbon) then well designed bearings should have a small barrier to sliding motion. Bearings made from curved (strained) structures should be feasible at some scale, regardless of the building block, because some degree of strain is always tolerable.

Alternatively, multiple single-linkage-group bearings could be aligned. Two building blocks with intercalating layers could have single rotationally free linkage groups between facing layers. As the layers are molecularly precise, perfect alignment of such single-linkage-group bearings from successive layers would be feasible, thus permitting a molecular bearing of tolerable strength (at least at the molecular scale) to be built.

Finally, a more traditional door-hinge type of joint could be built by using intercalating layers from the two halves of the joint. Rather than attempting to strain the building blocks to provide smooth surfaces, relatively large holes (many building blocks in diameter) could be made which were aligned from layer to layer. A tubular pin (possibly made from strained building blocks, or possibly of some other type, such as buckytubes) could then be inserted through the holes, in the expecation that the smooth surface of the pin would be sufficient to support hinge rotation.

While the use of strained building blocks is feasible, it would also be possible to use building blocks that were "pre-strained." For example, if a single edge atom in adamantane were changed from C to Si, the resulting building block would no longer be exactly tetrahedrally symmetric. Appropriately "malformed" building blocks could be used on specific crystal surfaces to relieve strain of a particular type. In addition, dislocations could be introduced into the structure. Special building blocks, designed specifically to relieve strain at the core of the specific dislocation, could be used to insure the stability (and feasibility) of the dislocation structure.

Rotary joints are of major importance for positional devices. It is possible to make a Stewart platform using nothing but appropriate rotary joints between otherwise rigid blocks. The design is left as an exercise for the reader -- though we note here that each of the six struts in a Stewart platform must support two degrees of freedom at each end, much as a universal joint, and one degree of rotational freedom along the axis of the strut (Merkle, 1997c). Powering movement of the platform by moving the ends of the struts opposite the platform is a separate issue that is not dealt with by this design -- though almost any powered one-degree-of-freedom movement of the "free" end of the strut would be sufficient.

Conclusions

Adamantane, C₁₀H₁₆, is a tetrahedrally symmetric stiff hydrocarbon that provides obvious sites for either four, six or more functional groups. Over 20,000 variants of adamantane have been synthesized, providing a rich and well studied set of chemistries.

As positional assembly of molecules has only recently been recognized as a feasible activity, prior research in this area has been limited. No serious barriers to further progress have been identified, quite possibly because serious barriers do not exist. Progress will, however, require substantial further research.

References

• Brenner, D.W. (1990) Phys Rev B, 42 No. 15, November 15, pages 9458-9471. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films
• Brenner, D.W.; Sinnott, S.B.; Harrison, J.A.; and Shenderova, O.A. (1996) Nanotechnology 7, pages 161-167. Simulated engineering of nanostructures
• Budavari, S.; et al. (1996) The Merck Index, Twelfth Edition, Merck, New Jersey.
• Dahl, J.E.; Moldowan, J.M.; Peters, K.E.; Claypool, G.E.; Rooney, M.A.; Michael, G.E.; Mello, M.R.; and Kohnen, M.L. (1999) Nature 399 pages 54-57. Diamondoid hydrocarbons as indicators of natural oil cracking.
• Drexler, K.E. (1992) Nanosystems: Molecular Machinery, Manufacturing, and Computation, Wiley.
• Drexler, K. E. (1994) Annual Review of Biophysics and Biomolecular Structure (23:337-405). Molecular machines: physical principles and implementation strategies.
• Drexler, K. E.; Peterson, C.; and Pergamit, G. (1991) Unbounding the Future: the Nanotechnology Revolution. William Morrow and Company, New York. Also available on the web at http://www.foresight.org/UTF/Unbound_LBW/chapt_4.html
• Ermer, Otto (1988) J. Am. Chem. Soc.110 3747-3754. Fivefold-diamond structure of adamantane-1,3,5,7-tetracarboxylic acid.
• Feynman, R.P. (1960) Caltech's Engineering and Science, February. There's Plenty of Room at the Bottom
• Fort, R.C. (1976) Adamantane: the chemistry of diamond molecules, Marcel Dekker.
• Hagerman, P.J. (1988) Ann. Rev. Biophys. Biophys. Chem. 17 pages 265-286. Flexibility of DNA.
• Halls, M.D. (1999) On the web at http://chem.wayne.edu/~mhalls/mbb/.
• Hutchison, K.; Gao, J.; Schick, G.; Rubin, Y.; Wudl, F. (1999) J. Am. Chem. Soc.1999, 121, 5611-5612. Bucky Light Bulbs: White Light Electroluminescence from a Fluorescent C60 Adduct - Single Layer Organic LED
• Jones, M.M., Gilkerson, W.R., Gallup, G.A. (1952) AIP. J. Chemical Physics 20, 1048. Hydrogen Bond Energies in Carboxylic Acids
• Jung, T.A., Schlittler, R.R., Gimzewski, J.K., Tang, H., and Joachim, C. (1996) Science 271, 181-184. Controlled room-temperature positioning of individual molecules: molecular flexure and motion
• Kim, P., and Lieber, C. M. (1999) Science "Nanotube Nanotweezers"
• Krummenacker, M. (1994) Chemical Design Automation News, Vol 9, September 1996. Steps towards molecular manufacturing
• Merkle, R.C. (1992) Journal of the British Interplanetary Society, 45, pages 407-413. Self replicating systems and molecular manufacturing
• Merkle, R.C. (1993a) Chemical Design Automation News, 8, Nos. 9 & 10, September/October. Molecular Manufacturing: adding positional control to chemical synthesis
• Merkle, R.C. (1993b) Nanotechnology 4, pages 86-90. A Proof about Molecular Bearings
• Merkle, R.C. (1996) Nanotechnology 7, pages 210-215. Design considerations for an assembler
• Merkle, R.C. (1997b) Nanotechnology 8, pages 23-28. Binding sites for use in a simple assembler
• Merkle, R.C. (1997c) Nanotechnology 8, pages 47-52. A new family of six degree of freedom positional devices
• Merkle, R.C. (1997d) Nanotechnology 8, pages 149-162. A proposed 'metabolism' for a hydrocarbon assembler
• Merkle, R.C. (1999) Trends in Biotechnology 17(7) pages 271-274. Biotechnology as a route to nanotechnology
• Mirkin, C.A., Letsinger, R.L., Mucic, R.C. and Storhoff, J.J. (1996) Nature 382, 607-09. A DNA-based method for rationally assembling nanoparticles into macroscopic materials.
• Musgrave, C.B.; Perry, J.K.; Merkle, R.C.; and Goddard, W.A. (1991) Nanotechnology 2, pages 187-195. Theoretical studies of a hydrogen abstraction tool for nanotechnology
• Qian W., Rubin Y. (1999) Angew Chem Int Ed Engl 1999 Aug;38(16):2356-2360 Towards Sixfold Functionalization of Buckminsterfullerene (C(60)) at Fully Addressable Octahedral Sites.
• Schoell, M. and Carlson, R.M.K (1999) Nature 399 pages 15-16. Diamondoids and oil are not forever.
• Seeman, N.C.; Zhang, Y.; and Chen, J. (1994) J. Vac. Sci. Technol. A 12(4), pages 1895-1903. DNA Nanoconstructions.
• Seeman, N.C. et al. (1997) The Fifth Foresight Conference on Molecular Nanotechnology. New Motifs In DNA Nanotechnology.
• Schwab, P.F.H.; Levin, M.D.; Michl, J. (1999) Chem. Rev. 99, pages 1863-1933. Molecular rods. 1. Simple axial rods.
• Sinnott, S.B.; Colton, R.J.; White, C.T.; and Brenner, D.W. (1994) Surface Science 316 pages L1055-L1060. Surface patterning by atomically-controlled chemical forces: molecular dynamics simulations
• Watson, J.D., Hopkins, N.H., Roberts, J.W., Steitz, J.A., Weiner, A.W. (1987) Molecular Biology of the Gene, Fourth Edition.
• Weast, R.C. et al. (1989) Handbook of Chemistry and Physics, 70th edition, CRC press.
• Zhang, Y.; and Seeman, N.C. (1994) Journal of the American Chemical Society 116, 1661-1669. The Construction of a DNA Truncated Octahedron