A New Family of Six Degree Of Freedom Positional Devices

Ralph C. Merkle
Xerox PARC
3333 Coyote Hill Road
Palo Alto, CA 94304
merkle@xerox.com
www.ralphmerkle.com

The final version of this article has been published in Nanotechnology Vol. 8, No. 2, June 1997 pages 47-52.

This is a draft. It is available on the web at http://www.zyvex.com/nanotech/6dof.html

More information about robotics is available on the web. Of particular interest is Jean-Pierre Merlet's pictorial survey of many positional devices.

Sandia has a page with further information on the use of Stewart platforms for machine tool use.

NIST has a gallery of pictures.

The Parallel Mechanisms Information Center has further information.

Robotics Online discusses Stewart platforms.

Abstract

Positional control is fundamental to most manufacturing processes as well as a wide range of other applications. Many types of positional devices have been proposed and used, ranging from robotic arms to Stewart platforms. This paper discusses a new family of six degree of freedom positional control devices which generally combine simple designs, high stiffness and strength, and a wider range of motion. Stiffness is particularly advantageous in very small (sub micron) positional devices as thermal motion is a significant source of positional uncertainty. The stiffness and thermally induced positional uncertainty of three designs -- a robotic arm, a Stewart platform, and one member of the new family -- are analyzed and compared. The Stewart platform provides the greatest stiffness for a given structural mass but has the most restrictive range of motion. The robotic arm is least stiff. The new proposal combines greater stiffness than the robotic arm with a significantly greater range of motion than the Stewart platform.

Introduction

Theoretical work in molecular manufacturing has highlighted the need for very small and very accurate manipulators which simultaneously have a wide range of motion, thus permitting the flexible assembly of molecular components (Drexler, 1992). The need for accurate positional control (a fraction of a nm (nanometer)) in the face of thermal noise implies the positional device must be stiff. The positional variance caused by thermal noise is k_BT/k m², where k_B is Boltzman's constant (in J/K or Joules/Kelvin), T is the temperature (in K), and k is the stiffness (spring constant) of the system in N/m (Newtons/meter). Scaling laws imply that stiffness is adversely affected by reductions in size and so stiffness is at a premium in small devices, particularly in devices that are molecular in scale yet must be able to position molecular components with an accuracy of a fraction of a nm. If we require a mean positional error of 2 x 10^-11 m (0.02 nm, 0.2 angstroms) the positional variance will be 4 x 10^-22 m². For k_BT = 4 x 10^-21 J (room temperature) this implies a stiffness of 10 N/m. This is acceptable for many of the proposed applications for molecular robotics. A molecular robotic device on the order of 100 nm in size should be capable of achieving such a stiffness (Drexler, 1992), but if we wish to achieve the best stiffness with the smallest atom count (a useful figure of merit for molecular robotic proposals) then the use of conventional robotic arms (or other serial linkage devices) would seem to be suboptimal. Parallel linkage devices are an attractive alternative, but the best known such device (the Stewart platform (Stewart, 1965)) has limitations in its range of motion. It would be useful to find designs which are compact, stiff, strong and provide a wider range of motion. These desiderata are not unique to molecular robotics. An analysis of the stiffness and thermally caused positional uncertainty of a conventional robotic arm, the Stewart platform, and the new proposal are in the section headed "Thermal noise."

The Stewart Platform

Figure 1: The Stewart Platform (illustration from Nanosystems, Drexler 1992)

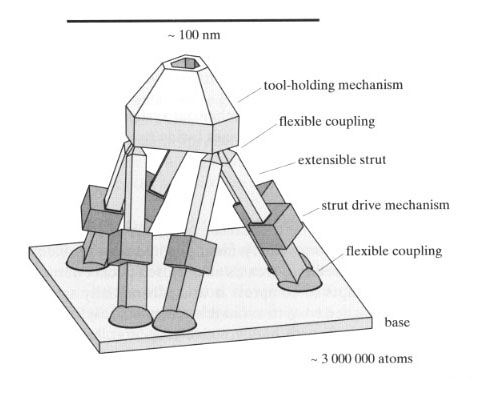
In its most basic form, the Stewart platform consists of an octahedron in which one triangular face is designated the "platform" and the opposing triangular face is designated the "base." The six struts of the octahedron that connect the base to the platform can be varied in length. The position and orientation of the platform with respect to the base will vary depending on the lengths to which the six struts are adjusted. Because there are six struts, the Stewart platform can be used to position the platform in six degrees of freedom. Although actually described earlier by (Gough, 1962) for use in tire testing, the term "Stewart platform" is more common and will be used here. Various methods of improving its range of motion have been proposed (no attempt will be made to summarize the literature in this area, a single illustrative reference is (Stoughton, 1993)). Three companies have introduced machine tools based on the Stewart platform: Ingersoll (Industry Week, 1993), Giddings & Lewis (Modic, 1994), and Hexel.

A 3-D VRML model of the Stewart platform is available on the web.

We propose a new family of positional devices which provide high stiffness and strength (like the Stewart platform) but with an increased range of motion.

The Double Tripod

Figure 2: The Double Tripod

The archetypal member of this class is the "double tripod" illustrated in figure 2. (A VRML model is available at http://www.zyvex.com/nanotech/vrml/tripod.wrl). Basically, the device is two tripods. The four small support struts support the two main struts. Each grouping of one main strut and its two attached support struts is one tripod of the double tripod. The tips of the two main struts then attach to a single shaft, shown at the top of the figure. The position and orientation of the shaft (which is analogous to the platform in the Stewart platform) is defined by the line segment between the tips of the two main struts. The rotational orientation about the axis of the shaft is defined by the length of this line segment.

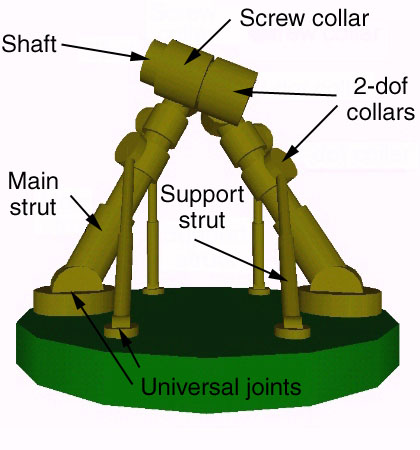
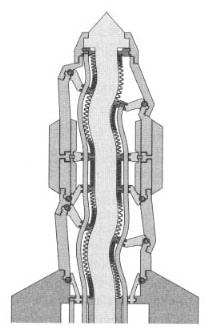
Figure 2 shows six struts attached to the base by six universal joints which each provide two degrees of freedom and allow the strut to point in any direction with respect to the base. The strut itself provides one degree of freedom, permitting the two ends of the strut to rotate with respect to each other (as would occur if it were hydraulically actuated).

Alternatively, the six struts could be attached to the base by six ball joints, providing the same three degrees of freedom.

The four support struts attach to the two main struts at what might be called "collars" that provide two degrees of freedom. The collars allow the support struts to point in any direction with respect to the main struts to which they attach. The right hand main strut attaches to the uppermost shaft by a similar collar joint which provides two degrees of freedom. The left hand main strut attaches to the shaft via a helical or screw collar. This provides two degrees of freedom, but couples rotation of the collar about the shaft to movement along the shaft. This might be done by providing the shaft with helical threads, much as a threaded bolt, and by constructing the helical collar much as one might construct a nut -- with threads inside which engage the threads on the shaft. By adjusting the pitch of these threads, the rotation of the shaft can be made either more or less sensitive to movement of the tip of the left main strut away from or towards the tip of the right main strut.

The six struts can be adjusted (by means not discussed in this paper) to any desired length within a certain range. The main struts might be extended or shortened either between the universal joint and the collar (a region we call the primary strut) or between the collar and the tip (which we call the stub). Either is possible. The tips of the two main struts can be forced to any arbitrary positions in three-space within a certain range of motion. The shaft can now be oriented in all six degrees of freedom, for it is held by a collar at one end that permits rotation (but not motion along the axis of the shaft) and by a screw collar at the other end that permits motion of the screw collar along the axis of the shaft but only when that motion is coupled with rotational motion of the shaft itself.

The range of motion of the double tripod can be understood intuitively by noting that within a wide range of motion the shaft can interact only with the main struts, and likewise that the support struts can interact only with their corresponding main struts. The support struts will not interact with each other under normal conditions of operation, i.e., if we keep the left tip and the right tip within a relatively short distance (the length of the shaft is not too long) and if we further keep the left and right tips above the ground plane. This arrangement reduces the number of strut-strut interactions that can limit motion.

The interaction between each main strut and its corresponding support struts will impose no limitations under the conditions described. The interactions between the two main struts and between each main strut and the shaft will impose only weak constraints on the range of motion. The shaft can easily be turned upside down, rightside up, oriented to the left or right, front or back, etc.

The Stewart platform has the desirable property that all six struts carry only compression or tension. The double tripod can result in bending forces being applied to the main struts. This disadvantage can be reduced by shortening the stub (i.e., the distance between the tips of the main struts and the collars that connect the supporting struts to the main struts). Reducing this distance, however, can reduce the range of motion of the double tripod as it might allow the struts in the two tripods to interact with each other. Further, the screw collar can apply an (independent) bending moment to the main strut to which it connects (though under normal conditions this should be relatively minor). Forces applied to the supporting struts can be purely compression or tension (though the illustrated collar design actually has the support struts attaching slightly off center of the main struts, which provides some improvement in the range of motion of the collar but only at the cost of slightly bending the support struts under load -- even this could be eliminated by using a different joint design).

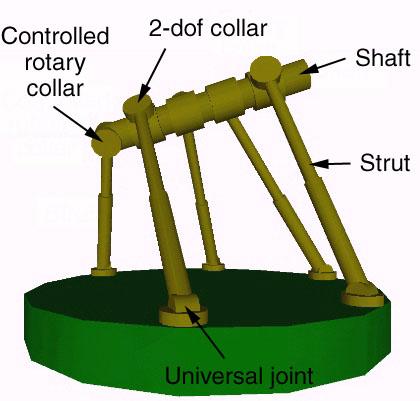
An obvious variation on this design would be to eliminate one of the support struts connected to the right main strut, and to replace the screw collar with a rotationally controlled collar. This might be called a five-thirds double tripod or just a five-thirds tripod. It would provide truly continuous rotary motion of the shaft.

The Crank

Figure 3: The Crank

Figure 3 illustrates a type of Stewart platform which replaces the conventional platfrom with a single bent shaft (the "crank"). A VRML model is available on the web. As in the Stewart platform, there are six struts that support the platform. The struts are connected to the shaft by six rotary collars. Because the collars allow the shaft to rotate completely, the shaft can rotate continuously. There are a wide range of possible shapes for the crank. In this approach, the radius of the shaft needs to be large to provide adequate stiffness, particularly if the shaft is long. This might add considerable mass to the crank. We do not analyze this issue in detail.

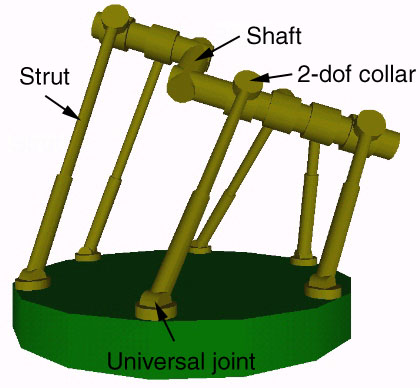
In a variation of this idea, we could use a straight shaft and replace one of the six rotary collars with a screw collar so that rotational motion of the shaft is coupled with linear motion of the screw collar along the shaft. By changing the length of the sixth strut, we could slide the screw collar along the shaft and rotate the shaft. This limits the rotational motion of the shaft around its axis, for after some distance the screw collar must reach the end of its range of motion along the shaft. By adusting the pitch of the screw, the number of rotations that the shaft can undergo can be adjusted.

Figure 4: Five-Strut Crank

In a third variation of this idea, we could use five struts (as illustrated in Figure 4) instead of six, connecting the struts to the shaft using four rotary collars and one rotationally controlled collar (e.g., motor driven). The position and orientation of the shaft can be controlled by adjusting the length of the five struts (as in a Stewart platform) and also the angular position of the one rotationally controlled collar. The shaft can be rotated continuously about its axis.

Again, a VRML model is available.

In all of the devices discussed the particular arrangement of joints can be varied. The universal joints could be replaced with ball joints (which provide an additional degree of rotational freedom) eliminating the need for a rotational degree of freedom along the strut. The attachment points of the struts could be varied along the length of the shaft and on the supporting structure.

While the crank permits continuous rotation of the shaft, in other respects its range of motion is not greatly dissimilar to that of the more usual type of Stewart platform (although the range of motion can be significantly altered by adjusting the placement of the collars along the shaft).

Thermal noise

In this section we consider the influence of thermal noise on the positional accuracy of the robotic arm, the Stewart platform and the double tripod. We start with a simplified analysis of a standard robotic arm. Basic to much of this section is the equation:

(1) positional variance = sigma²= k_BT/k

This equation, derived in (Drexler, 1992, chapter 5), relates stiffness k (in N/m) and thermal noise k_BT (in J) to positional variance sigma² (in m²) in one dimension. Sigma (= the mean displacement) is just the square root of the positional variance sigma². To use this equation, we must know k_BT and k. At room temperature, k_BT is about 4 x 10^-21 J. The stiffness k is related to the type and shape of the material in a complex way. We will consider simple examples where classical equations for stiffness are well known and derive approximate results which illustrate the basic issues.

The basic equation describing stiffness is:

(2) F = -k d

where F is the restoring force (in N) and d is the displacement (in m). Note that this equation is linear and assumes a perfectly elastic material (i.e., one that doesn't undergo permanent deformations when stretched). An excellent discussion of elasticity and the basic equations involved is given in (Feynman, 1964, Vol II, section 38).

The robotic arm

Figure 5 (illustration from Nanosystems, Drexler 1992)

The bending of a simple cantilevered rod with a circular cross section is described by:

(3) F = -(3 E I / L³) d = - [(3 pi r⁴ E) / (4 L³)] d

where:

d is the deflection of the end of the rod (transverse, not stretching) in m.
E is Young's modulus (10¹² Pa (Pascals) for diamond).
F is the restoring force in N.
I is the moment of inertia of the cross section in m⁴. For a circular cross section, I = pi r⁴ / 4.
L is the length of the rod in m.
pi is 3.14159....
r is the radius of the circular cross section in m.

As a consequence, the stiffness k for the transverse displacement of the end of such a rod is:

(4) k_displacement = ( 3 pi r⁴ E ) / (4 L³)

If we model a robotic arm by such a rod, then its positional variance can be derived by substituting (4) into (1) giving:

(5) ( k_BT 4 L³ ) / ( 3 pi r⁴ E )

A more detailed analysis is given in (Drexler, 1992), but for our purposes the simpler model will suffice.

The Stewart Platform

The great advanatage of the Stewart platform is that no bending forces are applied to its six struts: they are in pure tension or pure compression. As a consequence, we wish to know not their stiffness with respect to deflection of their ends but their stretching stiffness. This is given by:

(6) k_stretch = pi r² E / L

The positional variance of a single strut in a Stewart platform is given by subsituting (6) into (1) giving:

(7) k_BT L / ( pi r² E )

If we assume that the positional variance of the Stewart platform in any given direction is approximately equal to the positional variance of a single strut, then (7) also describes the approximate positional variance for the Stewart platform.

Equating (5) and (7) (i.e., comparing a robotic arm with a Stewart platform which has the same thermally induced positional uncertainty) lets us derive the relationship between the radius of a strut in a Stewart platform and the radius of a robotic arm of similar stiffness:

(8) r_stewart = r_arm² sqrt(3) / ( 2 L )

Which can also be expressed as:

(9) r_stewart / r_arm = ( sqrt(3) / 2 ) ( r_arm / L ) = 0.87 ( r_arm / L )

The smaller the value of (9), the less structural mass will be required in a Stewart platform compared with a robotic arm of similar stiffness. (9) makes it clear that the Stewart platform has the advantage when L is large and r_arm is small, i.e., when the robotic arm is long and slim. As the robotic arm becomes shorter and squater the advantage of the Stewart platform is reduced.

A final caution: we have assumed that the stretching of each strut in the Stewart platform is linear. However, in compression a strut can buckle. As a consequence, we would expect that under certain conditions the assumption of a linear restoring force would break down and our equations would give incorrect answers.

The critical buckling force for a rod is (Feynman, 1964):

(10) F_buckling = ( pi² E I ) / L²

where I is the moment of inertia for the particular cross section. For a rod (which has a circular cross section), I = pi r⁴ / 4, so the critical buckling force is:

(11) F_buckling = ( pi³ r⁴ E ) / ( 4 L² )

Substituting (6) and (11) into (2) we can deduce the displacement at which the rod will just start to buckle. Shortening the rod by more than this critical length will cause deviations from linearity. The critical displacement is:

(12) d_buckling = -(pi² r²) / (4 L)

Provided that the mean error in position is smaller than the buckling distance, our linear approximation for the response of the struts to thermal noise should be reasonable. As the mean error approaches the buckling distance, our approximation becomes increasingly suspect and our computed answer becomes increasingly distorted by the non-linear component of the restoring force.

A numerical example can provide some intuition. For:

L = 10^-7 m (100 nm)
positional variance sigma² = 10^-22 m² (i.e., the desired mean error in position, sigma, is 10^-11 m (0.1 angstroms))
E = 10¹² Pa (the Young's modulus of diamond)
k_BT = 4 x 10^-21 J (room temperature)

then by (7) we find the radius of one strut of the Stewart platform must be 1.1 nm while from (5) we find that the radius of a robotic arm able to provide similar stiffness is 11.4 nm. (This is only slightly smaller than the 15 nm external radius (Drexler, 1992) for the base of a robotic arm which, using more detailed calculations based on a specific design, had a mean positional error slightly larger than 10^-11 meters). The robotic arm thus has about a 10 times greater radius and 100 times greater cross sectional area than a single strut in a Stewart platform. From (12), we find that the critical buckling distance is about 0.030 nm, about 3 times the mean error, sigma, of 0.010 nm; suggesting that our answer will be somewhat but not greatly distorted by the non-linear nature of the restoring force for large deflections. The buckling force is slightly over 10^-9 N, so our Stewart platform would be able to apply forces up to about 10^-9 N. A very small increase in r would greatly increase both the stiffness and force.

The Double Tripod

The analysis of the double tripod combines the analysis of the Stewart platform and the robotic arm. The two main struts of the double tripod can bend, while the four support struts are in pure compression or tension.

Figure 6

Figure 6 shows a single main strut, attached at point P_attachment to the support struts. For clarity, the support struts are omitted from this figure. The curved line shows the behavior of the main strut when a force F_tip is applied transversely (straight down in the figure) to the tip. For clarity, this curve is exaggerated. Another force, F_base, is acting on the base of the strut at P_base.

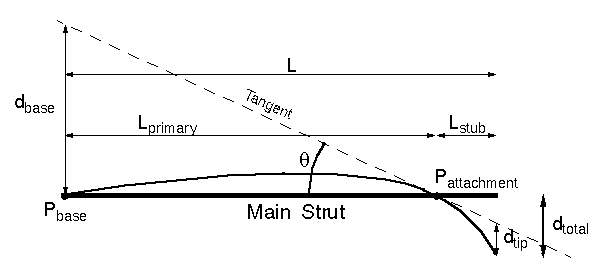
Because the angular motion around P_attachment is zero, the torque created by F_tip and F_base must be equal, or:

(13) F_tip L_stub = F_base L_primary

The line tangential to the main strut at P_attachment is a convenient reference from which to measure deflections. The stub and the primary can be viewed as two beams cantilevered from P_attachment and parallel at that point to the tangent line. The equations for these deflections (provided that theta is small) are similar to (3) and are:

(14) d_base = F_base (4 L_primary³) / ( 3 pi r_tripod⁴ E )

(15) d_tip = F_tip (4 L_stub³) / ( 3 pi r_tripod⁴ E )

The angle, theta, is arc sin ( d_base / L_primary ). For small theta, this is approximately:

(16) theta = d_base / L_primary

The total deflection of the tip is just the sum of d_tip and the angular deflection caused by theta and the distance L_stub:

(17) d_total = d_tip + L_stub sin ( theta ) = d_tip + L_stub theta

Combining equations (13) through (17) gives:

(18) d_total = F_tip ( 4 L_stub² L ) / ( 3 pi r_tripod⁴ E )

The stiffness of the tip with respect to deflection is therefore:

(19) k_tripod = ( 3 pi r_tripod⁴ E ) / ( 4 L_stub² L )

and the positional variance is given by:

(20) ( k_BT 4 L_stub² L ) / ( 3 pi r_tripod⁴ E )

This, however, neglects the contribution to positional uncertainty caused by the stretching of the support struts: this can be computed by using equation (7) with a radius equal to the radius of the support struts. (Provided L_stub is small compared with L, we can neglect the fact that the stretching of the support struts will actually be slightly magnified at the tip of the main strut by leverage). These positional variances are approximately additive, so the total positional variance of the double tripod is approximated by:

(21) ( k_BT 4 L_stub² L ) / ( 3 pi r_tripod⁴ E ) + k_BT L / ( pi r_support² E )

This approximation assumes that the stretching of the main strut can be neglected. When the length of the stub is long compared with the radius of the support struts, then (21) is dominated by the bending of the main strut. As the stub becomes short compared with the radius of the support struts, (21) is dominated by the stretching of the support struts.

As it is expected that the stub will normally be longer than the radius of the support struts, we can most easily determine the relationship between the radius of the main strut and the radius of a robotic arm of similar positional uncertainty by equating (20) (rather than 21) with (5) giving:

(22) r_tripod = sqrt( L_stub / L ) r_arm

While this will give inaccurate values when L_stub is smaller than r_support, it is a simpler and more intuitively meaningful expression than one derived by equating (21) with (5). Designing a double tripod with L_stub smaller than r_support is likely to be unusual. Equation (22) will also give inaccurate values when L_stub approaches L: this regime of operation is also expected to be rare.

Making L_stub almost as small as r_support will improve stiffness while keeping the total structural mass of the double tripod at a minimum. Increasing L_stub will sacrifice some stiffness but will increase the range of motion.

A numerical example can help to make these results more intuitive. If (as before) we wish a positional variance of 10^-22 meters² and a length L of 100 nm, and if L_stub = 10 nm and L_primary = 90 nm; then the radius of the main struts must be 3.6 nm. While not as good as the 1.1 nm radius of the struts in the Stewart platform, it is a definite improvement over the 11.4 nm radius of the robotic arm.

In summary: the double tripod shows improved stiffness when compared with conventional serial linkage manipulators (e.g., a robotic arm) and improved range of motion when compared with the Stewart platform. The tradeoff between stiffness and range of motion can be flexibly adusted by altering the positions of the attachment points of the support struts on the main strut. The closer the attachement points to the tip, the more closely the double tripod resembles a Stewart platform: its range of motion is reduced while its stiffness is increased. By moving the attachment point away from the tip (increasing the value of L_stub), we can increase the range of motion but only by decreasing the stiffness and increasing the thermal positional error.

It is worth emphasizing that the formulae in this section are approximate and are provided to illustrate trends and give an intuitive understanding of the tradeoffs involved. Specific systems are likely to differ from the results given here. A more detailed analysis would be required to determine the most advantageous approach in any specific design situation. Specific molecular systems are best analyzed using molecular mechanics and molecular dynamics.

Conclusions

Standard serial linkage positional devices, such as robotic arms, exhibit relatively low stiffness for a given mass. Parallel linkage devices such as the Stewart platform can provide much higher stiffness for a given structural mass. However, this increased stiffness is usually associated with a decreased range of motion. A novel design, the double tripod, provides greater stiffness for a given structural mass than a robotic arm, but has a significantly greater range of motion than a Stewart platform. The tradeoff between stiffness and range of motion in the double tripod can be continuously adjusted by altering simple design parameters. Simple analytical approximations to the stiffness of these three designs were developed, based on isotropic continuum models, which illustrate the quantitative tradeoffs both between the different designs and between the same design but with different design parameters.

References

Drexler, K.E., (1992) Nanosystems: molecular machinery, manufacturing, and computation, Wiley&Sons.
Feynman, R.P., Leighton, R.B., and Sands, M. (1964) The Feynman Lectures on Physics, Addison-Wesley.
Gough, V.E. and Whitehall, S.G., (1962) Universal Tyre Test Machine, Proc. 9th Int. Tech. Congress F.I.S.I.T.A., May, page 117.
Modic, S., (1994) Virtual Axis Machining: the shape of things to come?, Tooling & Production, July, pages 13-16.
Stewart, D., (1965-66) A Platform with Six Degrees of Freedom, The Institution of Mechanical Engineers, Proceedings 1965-66, 180 Part 1, No. 15, pp. 371-386.
Stoughton, R.S., and Arai, T. (1993) A Modified Stewart Platform Manipulator with Improved Dexterity, IEEE Transactions on Robotics and Automation, 9, pp. 166-173.
Technology of the Year: Ingersoll Milling Machine Co., Industry Week, December 20, 1993, pages 32-33.

This page is part of the nanotechnology web site.