Computational nanotechnology

by

Ralph C. Merkle
Xerox PARC
3333 Coyote Hill Road
Palo Alto, CA 94304
merkle@xerox.com

Nanotechnology is published by IOPP (the Institute of Physics Publishing).

Abstract

Introduction

The concept of a "Universal Constructor" is perhaps more recent. The concept was well understood by von Neumann in the 1940's, who defined a "Universal Constructor" in a two-dimensional cellular automata world. Such a model is a mathematical abstraction something like an infinite checkerboard, with several different types of "checkers" that might be on each square. The different pieces spontanesouly change and move about depending on what pieces occupy neighboring squares, in accordance with a pre-defined set of rules. Von Neumann used the concept of a Universal Constructor in conjunction with a Universal Computer as the core components in a self-replicating system[7]. The possibility of fabricating structures by putting "...the atoms down where the chemist says..." was recognized by Feynman in 1959[3]. Drexler recognized the value of the "assembler" in 1977. (Note: Drexler said "Though assemblers will be powerful ... they will not be able to build everything that could exist.") The assembler is analogous to von Neumann's Universal Constructor, but operates in the normal three dimensional world and can build a large, atomically precise structures by manipulating atoms and small clusters of atoms. He published the concept in 1981[8] and in subsequent work [6] has proposed increasingly detailed designs for such devices. The basic design of Drexler's assembler consists of (1) a molecular computer, (2) one or more molecular positioning devices (which might resemble very small robotic arms), and (3) a well defined set of chemical reactions (perhaps one or two dozen) that take place at the tip of the arm and are able to fabricate a wide range of structures using site-specific chemical reactions.

It is now common for forecasts of future technical abilities to include the ability to fabricate molecular devices and molecular machines with atomic precision[4, 11, 19].

While there continues to be debate about the exact time frame, it is becoming increasingly accepted that we will, eventually, develop the ability to economically fabricate a truly wide range of structures with atomic precision. This will be of major economic value. Most obviously a molecular manufacturing capability will be a prerequisite to the construction of molecular logic devices. The continuation of present trends in computer hardware depends on the ability to fabricate ever smaller and ever more precise logic devices at ever decreasing costs. The limit of this trend is the ability to fabricate molecular logic devices and to connect them in complex patterns at the molecular level. The manufacturing technology needed will, almost of necessity, be able to economically manufacture large structures (computers) with atomic precision (molecular logic elements). This capability will also permit the economical manufacture of materials with properties that border on the limits imposed by natural law. The strength of materials, in particular, will approach or even exceed that of diamond. Given the broad range of manufactured products that devote substantial mass to load-bearing members, such a development by itself will have a significant impact. A broad range of other manufactured products will also benefit from a manufacturing process that offers atomic precision at low cost.

Given the promise of such remarkably high payoffs it is natural to ask exactly what such systems will look like, exactly how they will work, and exactly how we will go about building them. One might also enquire as to the reasons for confidence that such an enterprise is feasible, and why one should further expect that our current understanding of chemistry and physics (embodied in a number of computational chemistry packages) should be sufficient to explain the operating principles of such systems.

It is here that the value of computational nanotechnology can be most clearly seen. Molecular machine proposals, provided that they are specified in atomic detail (and are of a size that can be dealt with by current software and hardware), can be modeled using the tools of computational chemistry.

There are two modeling techniques of particular utility. The first is molecular mechanics, which utilizes empirical force fields to model the forces acting between nuclei[9, 10, 15, 16, 17]. The second is higher order ab initio calculations, which will be discussed in a few paragraphs.

A few links to internet computational chemistry resources are provided here to provide those new to the area with some feel for what's available.

Molecular Mechanics

In molecular mechanics the individual nuclei are usually treated as point masses. While quantum mechanics dictates that there must be a certain degree of positional uncertainty associated with each nucleus, this positional uncertainty is normally significantly smaller than the typical internuclear distance. Bowen and Allinger[16] provide a good recent overview of the subject.

While the nuclei can reasonably be approximated as point masses, the electron cloud must be dealt with in quantum mechanical terms. However, if we are content to know only the positions of the nuclei and are willing to forego a detailed understanding of the electronic structure, then we can effectively eliminate the quantum mechanics. For example, the H₂ molecule involves two nuclei. While it would be possible to solve Schrodinger's equation to determine the wave function for the electrons, if we are content simply to know the potential energy contributed by the electrons (and do not enquire about the electron distribution) then we need only know the electronic energy as a function of the distance between the nuclei. That is, in many systems the only significant impact that the electrons have on nuclear position is to make a contribution to the potential energy E of the system. In the case of H₂, E is a simple function of the internuclear distance r. The function E(r) summarizes and replaces the more complex and more difficult to determine wave function for the electrons, as well as taking into account the inter-nuclear repulsion and the interactions between the electrons and the nuclei. The two hydrogen nuclei will adopt a position that minimizes E(r). As r becomes larger, the potential energy of the system increases and the nuclei experience a restoring force that returns them to their original distance. Similarly, as r becomes smaller and the two nuclei are pushed closer together, we also find that a restoring force pushes them farther apart, again restoring them to an equilibrium distance.

More generally, if we know the positions r₁, r₂, .... r_N of N nuclei, then E(r₁, r₂, .... r_N) gives the potential energy of the system. Knowing the potential energy as a function of the nuclear positions, we can readily determine the forces acting on the individual nuclei and therefore can compute the evolution of their position over time. The function E is a newtonian potential energy function (not quantum mechanical), despite the fact that the particular value of E at a particular point could be computed from Schrodinger's equation. That is, the potential energy E is a newtonian concept, but the particular values of E at particular points are determined by Schrodinger's equation.

Often called the Born-Oppenheimer approximation[13,20], this approach allows a great conceptual and practical simplification in the modeling of molecular systems. While it would in principle be possible to determine E by solving Schrodinger's equation, in practice it is usual to use available experimental data and to infer the nature and shape of E by interpolation. This approach, in which empirically derived potential energy functions are created by interpolation from experimental data, has spawned a wide range of potential energy functions, many of which are sold commercially. Because the gradient of the potential energy function E defines a conservative force field F, molecular mechanics methods are also called "force field" methods. While it is common to refer to "empirical force field" methods, the more recent use of ab initio methods to provide data points to aid in the design of the force fields[17] makes this term somewhat inaccurate, though still widely used.

The utility of molecular mechanics depends crucially on the development of accurate force fields. Good quality force fields have been developed for a fairly broad range of compounds including many compounds of interest in biochemistry[9, 10, 15, 16, 17]. While we will not attempt to survey the wide range of force fields that are available, one particular subset of compounds for which good quality force fields are available involve H, C, N, O, F, Si, P, S, Cl (and perhaps a few others) when they are restricted to form chemically uncomplicated structures (e.g., bond strain is not too great, dangling bonds are few or absent, etc). Many atomically precise structures which should be useful in nanotechnology fall in this class and can be modeled with an accuracy adequate to determine the behavior of molecular machines.

A potential energy function of particular utility in modeling diamondoid structures was described by Brenner (Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films, Donald W. Brenner, Phys Rev B, Vol. 42, No. 15, November 15 1990, pages 9458-9471). Brenner's potential energy function, though limited to the elements carbon and hydrogen, has the great advantage that it will handle transition states, unstable structures, and the like. Thus, given essentially arbitrary coordinates of the carbon and hydrogen atoms in a system, Brenner's potential will return the energy of the system. This permits molecular dynamical modeling of arbitrary hydrocarbon systems, including systems which use synthetic reactions involved in the synthesis of diamond. A particular reaction of interest is the selective abstraction of a chosen hydrogen atom from a diamond surface. See Surface patterning by atomically-controlled chemical forces: molecular dynamics simulations by Sinnott et al., Surface Science 316 (1994), L1055-L1060; see also the work of Robertson et al. for an illustration of the use of Brenner's potential in modeling the behavior of graphitic gears, including failure modes). Brenner has commented on the utility of this potential for modeling proposed molecular machine systems.

Of course, the "accuracy" of the force fields depends on the application. A force field which was accurate to (say) 10 kcal/ mole would be unable to correctly predict many properties of interest in biochemistry. For example, such a force field would lead to serious errors in predicting the correct three-dimensional structure of a protein. Given the linear sequence of amino acids in a protein, the protein folding problem is to determine how it will fold in three dimensions when put in solution. Often, the correct configuration will have an energy that differs from other (incorrect) configurations by a relatively modest amount, and so a force field of high accuracy is required.

Consider, however, the bearing illustrated in figures 1 and 2. Unlike the protein folding problem, where an astronomical range of configurations of similar energy are feasible, the bearing basically has only one configuration: a bearing. While the protein has many unconstrained torsions, there are no unconstrained torsions in the bearing. To significantly change any torsion angle in the bearing would involve ripping apart bonds. Thus, the same force field which is of marginal utility in dealing with strands of floppy protein is quite adequate for solid blocks of stiff diamondoid material. Not only will small errors in the force field still result in an accurate prediction of the global minima, (which in this case will be a single large basin in the potential energy surface) but also the range of possible structures is so sharply limited that little or no computational effort need be spent comparing the energies of different configurations. Long computational runs to evaluate the statistical properties of ensembles of configurations are thus eliminated.

Figure 1. A molecular bearing.

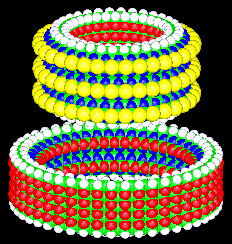
Figure 2. The bearing taken apart.

This observation, that the same force field that is inadequate for one class of structures is quite adequate for the design and modeling of a different class of structures, leads to a more general principle. Computational experiments generally provide an answer with some error distribution. If the errors produced by the model are of a similar size to the errors that would result in incorrect device function, then the model is unreliable. On the other hand, if the errors in the model are small compared with the errors that will produce incorrect device function, then the results of the model are likely to be reliable. If a device design falls in the former category, i.e., small errors in the model will produce conflicting forecasts about device function, then the conservative course of action is to reject the proposed design and keep looking. That is, we can deliberately design structures which are indeed adequately handled by our computational tools. As illustrated by the bearing, there are a wide range of basically mechanical structures whose stability is sufficiently clear and whose interactions with other structures is sufficiently simple that their behavior can be adequately modeled with currently available force fields.

An even stronger (although somewhat more subtle) statement is possible. The bearing illustrated in figures 1 and 2 is simply a single bearing from a very large class of bearings. The strain in the axle and the sleeve is proportional to the diameter of the bearing. By increasing the diameter, we can reduce the strain. Thus, we can design bearings in this broad class in which the strain can be reduced to whatever level we desire. Because we are dealing with what amounts to a strained block of diamond, the fact that we can reduce strain arbitrarily means that we can design a bearing whose local structure bears as close a resemblance to an unstrained block of diamond as might be wished. We can therefore be very confident indeed that some member of this class will perform the desired function (that of a bearing) and will work in accordance with our expectations. Given that we have developed software tools that are capable of creating and modeling most of the members of a broad class of devices, then we can investigate many individual class members. This investigation then lets us make rather confident statements about the functionality that members of this class can provide, even if there might be residual doubts about individual class members.

A moments reflection will show that the class of objects which are chemically reasonably inert, relatively stiff (no free torsions), and which interact via simple repulsive forces that occur on contact; can describe a truly vast class of machines. Indeed, it is possible to design computers, robotic arms and a wide range of other devices using molecular parts drawn from this class[1,2,5,6].

Ab Initio Methods

Several reactions mechanisms have been discussed, and a great many more are feasible.

Sufficiency of Current Modeling Methods

Clearly, not all molecular machines satisfy these constraints. Is the range of molecular machines which do satisfy these constraints sufficiently large to justify the effort of designing and modeling them? And in particular, can we satisfactorily model Drexler's assembler within these constraints?

The fundamental purpose of an assembler is to position atoms. To this end, it is imperative that we have models that let us determine atomic positions, and this is precisely what molecular mechanics provides. Robotic arms or other positioning devices are basically mechanical in nature, and will allow us to position molecular parts during the assembly process. Molecular mechanics provides us with an excellent tool for modeling the behavior of such devices.

The second fundamental requirement is the ability to make and break bonds at specific sites. While molecular mechanics provides an excellent tool for telling us where the tip of the assembler arm is located, current force fields are not adequate to model the specific chemical reactions that must then take place at the tip/work-piece interface involved in building an atomically precise part (though this statement must be modified in light of the work done with Brenner's potential, discussed above). For this, higher order ab initio calculations are sufficient.

The glaring omission in this discussion is the modeling of the kind of electronic behavior that occurs in switching devices. Clearly, it is possible to model electronic behavior with some degree of accuracy, and equally clearly molecular machines that are basically electronic in nature will be extremely useful. It will therefore be desirable to extend the range of computational models discussed here to include such devices. For the moment, however, the relatively modest inclusion of electrostatic motors as a power source is probably sufficient to provide us with adequate "design space" to design and model an assembler. While it might at first glance appear that electronics will be required for the computational element in the assembler, in fact molecular mechanical logic elements will be sufficient. Babbage's proposal from the 1800's clearly demonstrates the feasibility of mechanical computation[1] (it is interesting to note that a working model of Babbage's difference engine has been built and is on display at the British Museum of Science. They were careful to use parts machined no more accurately than the parts available to Babbage, in order to demonstrate that his ideas could have been implemented in the 1800's). Drexler's analysis of a specific molecular mechanical logic element[2] and further analysis of system design issues[6] also make it clear that molecular mechanical computation is sufficient for the molecular computer required in an assembler.

Molecular electronic proposals for computation have not been worked out as clearly at the system level as the molecular mechanical concepts[6]. Thus, at the moment, molecular mechanical proposals are better understood, at least in this particular context. This situation is likely to change, and when it does the electronic designs could be incorporated (where appropriate) into the design and modeling of an assembler. However, it is not entirely obvious that electronic designs will prove superior to molecular mechanical designs, particularly when device parameters such as size and energy dissipation are considered. While it seems virtually certain that electronic devices will prove faster than molecular mechanical devices, it is less obvious that electronic devices must necessarily be either smaller or dissipate less energy[5] (though confer more recent work on reversible logic). Indeed, given the difficulty of localizing individual electrons, it seems possible that electronic devices will prove to be inherently larger than molecular mechanical devices. This might provide a long term role for molecular mechanical devices as high density memory elements, or as logic elements when space (or atom count) is particularly constrained.

Whether the assembler is designed and built with an electronic or mechanical computer is less significant than designing and building it. By way of example, a stored program computer can be built in many different ways. Vacuum tubes, transistors, moving mechanical parts, fluidics, and other methods are all entirely feasible. Delaying the development of the Eniac because transistors are better than vacuum tubes would have been a most unwise course of action. Similarly, as we consider the design, modeling, and construction of an assembler, we should not hesitate to use simpler methods that we can understand in favor of better methods that are not yet fully in hand.

The methods of computational chemistry available today allow us to model a wide range of molecular machines with an accuracy sufficient in many cases to determine how well they will work. We can deliberately confine ourselves to the subset of devices where our modeling tools are good enough to give us confidence that the proposals should work. This range includes bearings, computers, robotic arms, site-specific chemical reactions utilized in the synthesis of complex structures, and more complex systems built up from these and related components. Drexler's assembler and related devices can be modeled using our current approaches and methods.

Molecular Compilers

Computational nanotechnology includes not only the tools and techniques required to model proposed molecular machines, it must also include the tools required to specify such machines. Molecular machine proposals that would require millions or even billions of atoms have been made. The total atom count of an assember might be roughly a billion atoms. While commerically available molecular modeling packages provide facilities to specify arbitrary structures, it is usually necessary to "point and click" for each atom involved. This is obviously unattractive for a device as complex as an assembler with its roughly one billion atoms. It should be clear that molecular CAD tools will be required if we are to specify such complex structures in atomic detail with a reasonable amount of effort. An essential development is that of "molecular compilers" which accept, as input, a high level description of an object and produce, as output, the atomic coordinates, atom types, and bonding structure of the object.

A simple molecular compiler has already been written at PARC, and was used to produce the bearing of figures 1 and 2. The specification of the axle was:

scale 0.9

tube     0 0.75 0.75   1.75 0 0   0 17 -17   0 5.25 5.25

grid     0 0.5 -0.5   0 1 1

delete   1.25  0 0

grid     0 0.25 0    0 0 0.25

change   O_3 to S_3  1.5 0 0

The second line begins with the "tube" specifier. This tells the program to produce a tubular structure, rather than a "block" or a "ring." the "ring" specifier is used to produce toroidal structures, e.g., tubes that have been further bent into donuts.

The first triplet of numbers following "tube," "0 0.75 0.75," specifies the offset to be used for the crystal lattice. The second triplet, "1.75 0 0" specifies that the surface of the tube is (100), and that the thickness of the tube wall is 1.75 lattice spacings. The third triplet, "0 17 -17," specifies the direction and length of the circumference of the tube. The direction [0 17 -17] (or [0 1 -1]) is at right angles to [1 0 0], the direction of the tube surface. The circumference of the tube is simply the length of the [0 17 -17] vector. Finally, "0 5.25 5.25" gives the direction of the axis and the length of the tube.

This does not fully specify the axle of the bearing, for the 100 surface has been cut circumferentially to produce grooves. The next command, "grid 0 0.5 -0.5 0 1 1" specifies that a grid is to be laid down on the surface. The grid is specified by two vectors, "0 0.5 -0.5" and "0 1 1,"" which give the directions and lengths of the edges of the unit parallelogram from which the grid is composed. The next command, "delete 1.25 0 0"" specifies that the point at coordinates "1.25 0 0" is to be deleted, and further, that all points in the same location with respect to any unit parallelogram of the grid are also to be deleted. Thus, this "grid .... delete ...." cuts out the grooves that are visible on the outer surface of the axle.

Finally, the commands "grid 0 0.25 0 0 0 0.25," and "change O_3 to S_3 1.5 0 0" are used to lay down a new, very fine grid that causes all oxygen atoms on the surface of the axle to be changed to sulfur.

A similar set of commands was used to specify the sleeve of the bearing.

It is easy to specify bearings with different surfaces, surface orientations, circumferences, lengths, etc. To select a (111), (110), (312), or any other surface, it is sufficient to change the vector that specifies the surface, and the vectors that specify the tangent to the surface and the axis of the tube (which must be at right angles to the surface vector). Thus, complex structures involving many atoms can be generated quickly and easily with a few lines of input specification.

The C source code is available at URL ftp://ftp.parc.xerox.com/pub/nano/tube.c. The program will generate output in either PolyGraf format or in Brookhaven format, so the output should be readable by most computational chemistry packages.

Conclusions

The author was part of a general purpose computer start up which successfully designed and built a new computer from scratch. This included the hardware, software, compilers, operating system, etc. During this process, extensive use was made of computational models to verify each level of the design. The operating system was written in Pascal, and checked out on another computer. The compilers were written in Pascal, and also checked out on another computer. The code produced by the compilers was checked out on an instruction set simulator. The microcode was checked out on a micro-instruction simulator. The logic design was checked out with logic level simulation tools, and circuit simulation packages were used to verify the detailed electronic design. All this work was done at the same time. The software was written and debugged even though the machine on which it would eventually be executed didn't exist. The microcode was written and debugged before the hardware was available. When the hardware was finally made available, system integration went relatively rapidly.

Imagine, for a moment, how long it would have taken to develop this system had we carried out the development in the obvious sequential fashion. First, we would have implemented the hardware and only then begun work on the microengine. Later, with the hardware and microengine fully checked out and working, we could have developed and debugged the microcode. With this firmly in hand, we could then have written the compilers and verified the code they produced. Finally, we could have implemented and checked out the operating system. Needless to say, such a strategy would have been very slow and tedious.

Doing things in the simple and most obvious way often takes a lot longer than is needed. If we were to approach the design and construction of an assembler using the simple serial method, it would take a great deal longer than if we systematically attacked and simultanesouly solved the problems that arise at all levels of the design at one and the same time. That is, by using methods similar to those used to design a modern computer, including intensive computational modeling of individual components and sub- systems, we can greatly shorten the time required to design and build complex molecular machines.

This can be further illustrated by considering the traditional manner of growth of our synthetic capability over time (figure 3). Today, we find we are able to synthesize a certain range of compounds and structures. As time goes by, we will be able to synthesize an ever larger range of structures. This growth in our ability will proceed on a broad front, and reflects the efforts of a broad range of researchers who are each pursuing individual goals without concern about the larger picture into which they might fit. As illustrated in figure 4, given sufficient time we will eventually be able to synthesize complex molecular machines simply because we will eventually develop the ability to synthesize just about anything.

However, if we wish to develop a particular kind of device, e.g., an assembler, then we can speed the process up (as illustrated in figure 5) by conducting computational experiments designed to clarify the objective and to specify more precisely the path from our current range of synthetic capabilities to the objective. Such computational experiments are inexpensive, can provide very detailed information, are possible for any structure (whether we can or cannot synthesize it) and will, in general, reduce the "time to market" for the selected product.

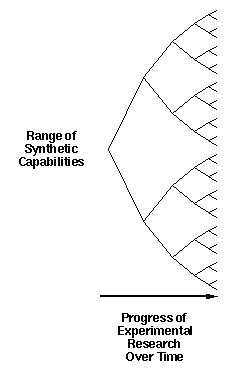
Figure 3. Experimental advances in our synthetic capabilities

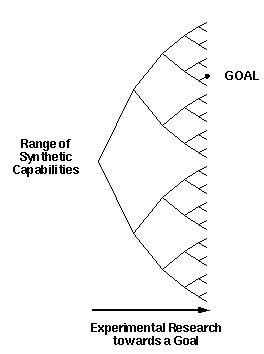
Figure 4. Experimental progress towards a goal

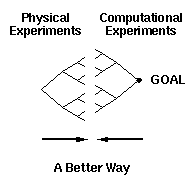
Figure 5. A more efficient method of achieving a goal

Computational experiments also provide more information. For example, molecular dynamics can literally provide information about the position of each individual atom over time, information which would usually be inaccessible in a physical experiment.

Of course, the major advantage of computational experiments over physical experiments in the current context is the simple fact that physical experiments aren't possible for molecular machines that we can't make with today's technology. By using computational models derived from the wealth of experimental data that is available today, we can (within certain accuracy bounds) describe the behavior of proposed systems that we plan to build in the future. If we deliberately design systems that are sufficiently robust that we are confident they will work regardless of the small errors that must be incurred in the modeling process, we can design systems today that we will not be able to build for some years, and yet still have reasonable confidence that they will work.

By fully utilizing the experience that has been developed in the rapid design and development of complex systems we can dramatically reduce the development time for molecular manufacturing systems. It is possible to debate how long it will be before we achieve a robust molecular manufacturing capability. However, it is very clear that we'll get there sooner if we develop and make intelligent use of molecular design tools and computational models. These will let us design and check the blueprints for the new molecular manufacturing technologies that we now see on the horizon, and will let us chart a more rapid and more certain path to their development.

Acknowledgements

References

• 1.) Of the Analytical Engine, by Charles Babbage, 1864, in: Perspectives on the Computer Revolution, by Zenon W. Pylyshyn, Prentice Hall, 1970.
• 2.) Rod Logic and Thermal Noise in the Mechanical Nanocomputer, by K. Eric Drexler, in Proceedings of the 3rd International Symposium on Molecular Electronic Devices, F.L. Carter, R.E. Siatkowski, H. Wohltjen, eds., North-Holland 1988.
• 3.) There's Plenty of Room at the Bottom, a talk by Richard Feynman at an annual meeting of the American Physical Society given on December 29, 1959.
• 4.) A Small Revolution Gets Under Way, by Robert Pool, Science, Jan. 5 1990.
• 5.) Two Types of Mechanical Reversible Logic, by Ralph C. Merkle.
• 6.) Nanotechnology: molecular machinery, manufacturing, and computation, by K. Eric Drexler, Wiley 1992.
• 7.) Theory of Self-Reproducing Automata, by John von Neumann, edited and completed by Arthur W. Burks, University of Illinois Press, 1966.
• 8.) Molecular engineering: An approach to the development of general capabilities for molecular manipulation, by K. Eric Drexler, Proceedings of the National Academy of Sciences U.S.A. 78(9): 5275-5278, 1981.
• 9.) Molecular Mechanics, by Ulrich Burkert and Norman L. Allinger, ACS Monograph 177, American Chemical Society, 1982.
• 10.) DREIDING: A Generic Force Field For Molecular Simulations, by Stephen L. Mayo, Barry D. Olafson, and William A. Goddard III, The Journal of Physical Chemistry, 1990, 94, pages 8897-8909.
• 11.) New Frontiers in Computing and Telecommunications, by J. A. Armstrong, IBM Vice President for Science and Technology and Chief Scientist, Creativity, June 1991, Vol 10 No. 2, pages 1-6.
• 13.) Methods of Molecular Quantum Mechanics, by R. McWeeny, Second Edition, Academic Press 1989.
• 14.) Theoretical studies of a hydrogen abstraction tool for nanotechnology, by Charles B. Musgrave, Jason K. Perry, Ralph C. Merkle, and William A. Goddard III, Nanotechnology.
• 15.) Reviews in Computational Chemistry, Vol 2, Kenny B. Lipkowitz and Donald B. Boyd, VCH Publishers, 1991.
• 16.) Molecular Mechanics: The Art and Science of Parameterization, by J. Phillip Bowen and Norman L. Allinger, page 81-97 of reference [15].
• 17.) New Approaches to Empirical Force Fields, by Uri Dinur and Arnold T. Hagler, pages 99-164, reference [15].
• 18.) Perspectives on the Computer Revolution, Zenon W. Pylyshyn, Prentice Hall 1970.
• 19.) Atom by Atom, Scientists Build `Invisible' Machines of the Future, by Andrew Pollack, The New York Times Science Section, Tuesday, November 26, 1991, page B7.
• 20.) The Nuclear Motion Problem in Molecular Physics, by B. T. Sutcliffe, in Advances in Quantum Chemistry, Vol. 28, 1997, pages 65-80. (This reference added 97.08.31).

This page is part of the nanotechnology web site.