Theoretical studies of diamond mechanosynthesis reactions.

Stephen P. Walch

Thermosciences Institute

NASA Ames Research Center

Moffett Field, CA 94035-1000

and

Ralph C. Merkle

Xerox, PARC

3333 Coyote Hill Road

Palo Alto, CA 94304

This paper is available on the web at http://www.zyvex.com/nanotech/mechanosynthesis.html. It was published in Nanotechnology 9 (1998) pages 285-296. The published version differs in some respects from this web page.

Abstract

Density functional theory methods have been used to examine the interaction of i) the carbene and C₂ tools with a pair of radical sites on the diamond (111) surface and ii) the carbene tool with a surface dimer on the reconstructed diamond (100) surface.

For the (111) surface, the carbene tool (carbenecyclopropene) is found to bond preferentially to a single radical site (on top site) rather than at a bridged site. This means this tool is not useful for adding a carbon to diamond (111). The C₂ tool, on the other hand, is found to add a bridged C₂ molecule, through a series of steps which are overall exothermic. The carbene tool can add a carbon to the bridged C₂ molecule, leading to a bridged C₃ molecule perpendicular to the surface, by an overall exothermic series of steps. If another radical site is activated, the C₃ can bend over to a three fold coordinated position, with only a small barrier. Thus, this series of steps can be used to create a three fold coordinated C₃ molecule on the diamond (111) surface.

For the surface dimer on the reconstructed (100) surface, the carbene tool is found to add with no barrier if the angle between the tool and the surface is allowed to vary or with a 0.09 aJ (13 kcal/mol) barrier for a C_2v constrained approach. In this case, a bridged site is strongly favored, and the subsequent steps of sequentially breaking the p and s bonds between the tool and added carbon atom are all feasable. Thus, this series of steps can add a bridged C atom to the reconstructed diamond (100) surface.

I. Introduction.

Manufactured products are made by arranging atoms. Current manufacturing methods provide limited control over the position of individual atoms in the final product. A manufacturing technology able to precisely arrange atoms in patterns chosen to enhance material properties and capabilities, rather than in the limited range of patterns that current manufacturing methods allow, would permit revolutionary improvements in product performance and capabilities. A material which in theory provides particularly attractive capabilities is diamond. Its advantages for electronic applications have been known for some time (Geis and Angus, 1992). Its strength-to-weight ratio is over 50 times that of metals used in aerospace applications and would permit major performance improvements in such applications (McKendree, 1996). One defect of diamond as a structural material (in addition to high manufacturing cost with current technology, which has been addressed by other authors (Drexler, 1992; Merkle, 1994) and will not be considered here) is it's inherent brittleness. However, modified structures related to diamond should retain most of the high strength while not being brittle. Since it isn't yet possible to make molecularly precise materials with todays technology, theory and modelling can play an important role in evaluating the properties of proposed new materials.

Conventional methods (e.g., CVD (Celii and Butler, 1991)) are unable to synthesize diamond with the precision envisioned here. As no immediately experimentally accessible approach appears able to achieve this objective, the use of theoretical methods and in particular quantum chemistry methods become indispensable if we are to examine and evaluate proposals. A general proposal advanced by Drexler (Drexler, 1992) is to use mechanical forces to position atoms and molecules in precise locations using a small robotic arm. Drexler proposed some molecular tools along with a few specific reactions utilizing those tools which could be used to synthesize diamond and related structures. One such tool was the carbene insertion tool (Fig. 1a), which Drexler suggested could be used on the diamond (110) surface. Application of the carbene tool to the (100) surface also appears plausible. The hypothesis that this tool might be useful on the (111) surface has not been investigated before, and interaction of the carbene tool with the (111) and reconstructed (100) surfaces are examined here. In addition, we examine the interaction of the C₂ tool with the (111) surface.

A hypothetical application of the carbene insertion tool to the (111) surface is shown in a sequence of steps for adding a C atom to the diamond (111) surface, illustrated in Fig. 2. The first step (Fig. 2a-b) is use of a hydrogen abstraction tool ( an alkynyl radical) (Musgrave, Perry, Merkle, and Goddard, 1991) to abstract two adjacent surface H atoms leading to two adjacent radical sites ( referred to as dangling bonds). The second step (Fig. 2b-c) is an insertion of the carbene tool leading to a bridged structure. The last step (Fig. 2c-d) is application of torque to break the CC p bond followed by application of force to break the remaining single bond between the carbene carbon and the cyclopropene ring, leaving a bridged carbon atom behind on the surface.

Theory can answer a number of questions related to the reactions in Fig. 2. A key issue is the nature of the interaction between a carbene and two adjacent dangling bonds on the surface. The dangling bonds on the surface are separated by 0.252 nm (2.52 Å) compared to a CC distance of 0.121 nm (1.21 Å) in acetylene, and it is not clear if for this CC distance it is energetically more favorable for the carbene to bridge accross two surface carbon atoms or to bond to just one surface carbon atom. If the latter is more favorable, then there are no restraining forces to permit breaking the CC p bond by application of torque, and subsequent application of force would simply reverse the addition process. If, on the other hand, bridging is favored, it is well established that carbene insertion proceeds by a pathway involving edge on approach, and it is not clear what the barrier would be for addition in the Woodward-Hoffman forbidden perpendicular approach as shown in Fig. 2.

Fig. 3 shows two reactions for vinylidene (CCH₂). The first ( Fig. 3a) is addition of the carbene pair to a p orbital of acetylene. This is analagous to to the pathway above leading to a bridged carbene on the surface. The second reaction (Fig. 3b) is the addition of a radical (in this case H atom) to vinylidene leading to vinyl radical. This is analagous to the pathway above leading to bonding to a single surface carbon atom. The vinylidene plus acetylene reaction will be used as a calibration for the DFT method since there are accurate ab initio calculations available for this system (Walch and Taylor, 1995).

In this paper we use density functional theory methods to investigate the interaction of several mechanosynthesis tools with the diamond (111) and reconstructed (100) surfaces using a cluster model.

II. Computational Details.

The calculations were carried out with the density functional theory(DFT) method with the Becke-3LYP functional and the 6-31G basis set using the program system G94. The clusters for the (111) surface are frozen at the bulk diamond geometry For the reconstructed (100) surface, the first layer is allowed to relax [ (2x1) dimer reconstruction) ], but the deeper layers are frozen at the bulk geometry. The first and second nearest neighbor distances are taken as 0.1545 nm (1.545 Å) and 0.2522 nm (2.522 Å), respectively.

III. Discussion.

a. Cluster model for diamond (111).

Fig. 4 shows the two clusters which were used. The larger cluster has three carbon atoms in the surface layer and six carbon atoms in the second layer. These 9 carbon atoms are located at the positions appropriate to the unreconstructed diamond (111) surface. The bonds between the second layer carbons and the other carbons, which are not included in the cluster, are simulated by CH bonds, where the CH bond has a bond length of 0.11 nm (1.1 Å) and is directed toward the appropriate bulk carbon atom. The smaller cluster has two surface carbon atoms and one second layer carbon atom with the bonds to the remaining bulk carbons simulated by CH bonds as was done for the larger cluster. The larger cluster has three surface dangling bonds and the smaller cluster has two surface dangling bonds. In the calculations the dangling bonds which are not involved in the reaction are also bonded to an H atom. In the following the larger cluster is denoted by cluster and the smaller cluster is denoted by cluster2.

An important question is the amount of interaction between two surface dangling bonds. This was quantified by computing the overlap between the two radical orbitals in a GVB(pp) calculation (for cluster2). The overlap is found to be only 0.016 and the triplet state is found to be 0.03 aJ (3.7 kcal/mol) below the singlet state. This result indicates that the dangling bonds may be thought of as localized radicals with only weak interaction with adjacent dangling bonds.

b. Cluster model for reconstructed diamond (100).

The unreconstructed diamond (100) surface has rows of surface carbon atoms which are carbene like, i.e they have two bonds to the second layer and two unsatisfied valences. Relaxation of the surface layer leads to a reconstructed surface with rows of dimers. Fig. 5 shows a cluster for one surface dimer on the diamond (100) surface. This cluster has two surface, four second layer, two third layer, and one fourth layer carbon atoms, respectively. The atoms in the second through fourth layers were held at the bulk positions and the dangling bonds are tied off with H atoms. The two surface layer atoms were allowed to relax in a density functional theory (DFT) calculation. In the dimer there is a radical orbital on each C atom, and these orbitals can be combined into singlet or triplet spin states. The simplest picture is that both states have a CC s bond and the singlet state has a weak p bond as well. An important question, which has been considered in the literature (Weiner, Skokov, and Frenklach, 1995.) is the amount of p bonding in the dimer. This may be quantified in various ways; perhaps the best way is to compute the overlap between the two radical orbitals in a GVB(pp) calculation. First the dimer geometries were computed for the singlet and triplet spin states using DFT. This gives a CC bond length of 0.1421 nm (1.421 Å) for the singlet and 0.1714 nm (1.714 Å) for the triplet. At the DFT singlet geometry, a GVB calculation gives an overlap of the radical orbitals of 0.462. These properties indicate a weak p bond. Another indication of the amount of p bonding is the singlet --> triplet excitation energy which is computed to be about 0.07 aJ (10 kcal/mol).

c. Structure of the carbene tool.

The carbene tool, shown in Fig. 1, was simulated by the case where the two R groups are H (C₄H₂). One question that arose was the relative energetics and barrier to isomerization between the three membered ring (carbenecyclopropene) and four membered ring ( 1,2-dehydro-cyclobutadiene) forms of C₄H₂. This question could be answered by high level ab-initio theory. Calculations using the CASSCF/ ICCI method for structures optimized at the CASSCF level and including zero-point effects estimated from the harmonic frequencies show that the carbene cyclopropene isomer is more stable by 0.20 aJ (29.4 kcal/mol). (See Table I. and Fig. 6) Thus, isomerization to the four membered ring form is unlikely at low temperatures. One reason for the low stability of 1,2-dehydro-cyclobutadiene is that the in plane p bond, that can be formally drawn, is very weak because of the approximately 90° CCC angle. (Compare to the surface dimer on the reconstructed diamond (100) surface discussed in section IIIb.)

The carbenecyclopropene form of the carbene tool has a singlet ground state. The lowest triplet state has the two radical orbitals in plane (a₁ and b₂ in C_2v symmetry) and is computed to be 0.31 aJ (44.3 kcal/mol) higher at the CASSCF level (0.30 aJ (42.6 kcal/mol) for DFT). The location of this triplet state is important, since the C_2v constrained insertion into a p bond (e.g. of a surface dimer on the reconstructed (100) surface) involves crossing of the surface arising from the ground states of the tool and cluster with the surface arising form the triplet states of the tool and cluster.

d. Structure of the C₂ tool.

Fig. 7 shows an isomerization pathway for the C₂ tool. The energetics are obtained with the CASSCF/ ICCI method as was done for the carbene tool. (See Table II.) Here it is seen that the carbene form ( 5 membered ring) is more stable than the six membered ring form by 0.10 aJ (15.1 kcal/mol). However, there is a barrier of 0.11 aJ (16.2 kcal/mol) between the two forms. Thus, the six membered ring form, which is the C₂ tool, is a stable minimum on the potential energy surface, and should have a useful lifetime at low temperatures. As for the carbene tool, we are also interested in the location of the triplet state of this tool. CASSCF finds the singlet state to be 0.09 aJ (10.3 kcal/mol) below the triplet state. This is about the same as for a surface dimer on the reconstructed (100) surface, and is consistent with an activated CC p bond.

e. Comparison of energetics for vinylidene plus acetylene reaction.

Calibration calculations have been carried out for several systems using both DFT and ab-initio methods. Table III shows energetics for several structures in the addition of vinylidene to acetylene ( Fig. 3a). The entrance channel barrier (sp1) is found to be 0.01 aJ (1.7 kcal/mol) compared to 0.04 aJ (5.4 kcal/mol) for ab initio. The structure min2 is found to be 0.40 aJ (58.0 kcal/mol) below reactants compared to 0.37 aJ (53.6 kcal/mol) for ab initio. Since the ab-initio values use double-zeta quality basis sets it is expected that the ab initio values would become closer to the DFT values if larger basis sets were used; i.e. the barrier height should decrease and the binding energy of min2 with respect to reactants should increase. Thus, the comparison here suggests that the DFT method reproduces the ab inito results well enough to be used for the calculations planned here, which seek to answer semi-quantitative issues.

f. Energetics for CH₃ + vinylidene.

The vinylidene plus acetylene reaction serves as a model for two adjacent surface radical sites (dangling bonds) which are close enough to have a significant amount of singlet pairing (this is appropriate e.g. for dimer sites on the reconstructed diamond (100) surface). In the opposite extreme, where the adjacent radical sites are too far apart to interact significantly (diamond (111) surface), the interaction with a carbene is like the interaction of a simple radical with a carbene. One example of such an interaction is the reaction of methyl radical (CH₃) with vinylidene (CCH₂) (Fig. 3b). Table IV shows energetics for this reaction at the ICCI level of theory. Here it is seen that the barrier for addition of the CH₃ radical to the carbene pair of vinylidene is only 0.002 aJ (0.3 kcal/mol). Thus, this process is predicted to be more facile than insertion into a CC p bond in acetylene.

g. Addition of the carbene tool (C₄H₂) to the diamond (111) surface.

Table V shows energetics for bonding the carbene tool to the two cluster models of diamond (111). Min1 is obtained by bonding the carbene tool to a cluster with only one radical site. Thus, this forces the system to go to a structure like Fig. 3b, arising by addition of a radical orbital to the carbene pair of the carbene tool (on top site). Min2 is the bridged site over two adjacent radical sites. Finally, min3 is a structure like min1 except that there is also an adjacent radical site. From Table V and Fig. 8. It is seen that the on top site is favored over the bridged site for diamond (111). It is also seen that the binding energies for min1 and min3 are very similar, which indicates that the adjacent radical site is only weakly interacting with the carbene tool bonded at an on top site. In Fig. 8, a barrier is shown separating min2 and min3. The saddle point for this process was not found. Min2 was obtained as a singlet state, while min3 was obtained as a triplet state. This is reasonable, since for min3 the triplet state should be nearly degenerate with the open shell singlet state. The failure to find a saddle point connecting min2 and min3 on the singlet surface is not surprising, since for an ab initio wavefunction this would involve a complex recoupling of the electron spins, which is a process which may not be well described by DFT.

These results indicate that the process depicted in Fig. 2 is not likely to work for diamond (111), since for the favored on top site there would be no restraining forces to oppose the applied torque to break the CC p bond. From comparison of the energetics with the two clusters, it is seen that the smaller cluster (cluster2) gives results in semiquantitative agreement with those obtained with the larger cluster. This is consistent with the rapid convergence with cluster size typically seen for covalently bound clusters.

h. Addition of the C₂ tool (C₄H₂O₂) to diamond (111).

The C₂tool (Fig. 1b) may be thoght of as a C₂ molecule bonded to glyoxal. As discussed in section IIId, bonding to glyoxal considerably activates the in plane CC p bond, since the OCCO framework is strongly bent leading to in plane radical orbitals, which are directed at approx 120° angles with respect to the CC bond. Thus, the overlap between these radical orbitals is low (comparable to the dimer on the reconstructed (100) surface, where the overlap of the two p orbitals is 0.462). The C_2v constrained approach of the C₂ tool to a pair of adjacent radical orbitals on the (111) surface is a Woodward-Hoffman forbidden process, which involves the crossing of the ground state surface with the surface arising from the triplet states of the tool and the cluster. In this case, the triplet state of the tool is 0.07 aJ (10 kcal/mol) above the singlet, while the triplet state of the surface is 0.03 aJ (4 kcal/mol) below the singlet state. Thus, the excitation energy to the upper surface is 0.04 aJ (6 kcal/mol), at infinite separation. Combining these considerations, addition of the C₂ tool accross two surface dimers on the (111) surface is expected to be a barrier-less process. This is what the calculations show, and the lack of a barrier is depicted in Fig. 9 as a straight line going down to the complex. The binding energy between the C2 tool and the surface is computed to be nearly 1.39 aJ (200 kcal/mol) ( 1.39 aJ (199.8 kcal/mol) and 1.30 aJ (187.4 kcal/mol) with cluster2 and cluster, respectively). (See Table VI.) The dissociation process in which a glyoxal comes off and leaves a C₂ behind has only a slight barrier with respect to products ( about 0.01 aJ (1 kcal/mol) ). As expected, the glyoxal has to tip out of plane in order to dissociate to the ground state. Overall the reaction is exothermic by about 0.69 aJ (100 kcal/mol) ( 0.69 aJ (98.9 kcal/mol) and 0.63 aJ (90.5 kcal/mol) with cluster2 and cluster, respectively). These calculations indicate that the C₂ tool will be effective in adding a bridged C₂ species to the diamond (111) surface.

i. Diamond (111) + bridged C₂ plus carbene tool.

Fig. 10 and Table VII show the interaction between a C₂ bridged on diamond (111) and the carbene tool. In this case bridged bonding is favored over bonding to one C of the bridged C₂. This reflects a situation in which the two surface radical orbitals, which correspond to the two electrons of the bent CC p bond, are more strongly interacting than in the case of adjacent radical sites on diamond (111). As for the results shown in Fig. 8, min2 was calculated as a singlet while min3 was calculated as a triplet. Fig. 11 and Table VII also show the energetics for the process cluster2 + C₂ plus carbene tool going to cluster2 + C3 + cyclo-C₃H₂. Here min1 is the bridged structure depicted in Figs. 7 and 8 and is bound by 0.68 aJ (97.5 kcal/mol). Min3 is the case where the carbene tool bonds to one C of the bridged C₂ as depicted in Fig. 7 and is bound by 0.62 aJ (88.8 kcal/mol) Min2 is the structure where the cyclopropene moity is twisted 90° such that the CC p bond is broken. This is still bound by 0.30 aJ (43.4 kcal/mol) with respect to reactants. Finally, the products, a bridged C₃ and cyclo-C₃H₂, are bound by 0.22aJ (31.1 kcal/mol) with respect to reactants. Thus, these calculations suggest that use of the C₂ tool followed by use of the carbene tool is a viable reaction sequence to put a C₃ on the diamond (111) surface.

j. Rearangement of chemisorbed C₃.

The previous sequence resulted in a C₃ unit sitting perpendicular to the diamond (111) surface. Fig. 12 and Table VIII show the energetics for a reaction pathway leading to a cyclic C₃ unit bridged across a three fold site on diamond (111). The barrier to this process is only 0.06 aJ (8.4 kcal/mol).

k. Addition of the carbene tool to a surface dimer on the reconstructed diamond (100) surface.

As discussed in section IIIb, a dimer on the reconstructed (100) surface has an activated p bond, but still has a significant amount of p bonding. Thus, the addition of a carbene (such as the C₂ tool) to this surface has some of the features of the addition of vinylidene to acetylene, which is depicted in Fig. 3a. (See also Walch and Taylor, 1994.) The lowest energy pathway is shown in Fig. 13. Here it is seen that this is a somewhat typical carbene insertion pathway, in that the carbene approaches in a parallel orientation to the CC p bond. One feature which is peculiar to this system is that the carbene approaches to the outside of the CC p bond. This approach results from the approximately 120° angles which the GVB orbitals of the p bond make with the CC bond. From Fig. 13 it is seen that the pathway initially is dominated by shortening of the forming CC bond, but then switches to mainly an angular change to give ultimately a bridged carbene structure. This pathway has no barrier.

The C_2v constrained approach is expected to have a barrier. The upper state in the curve crossing leading to this barrier arises from the triplet states of the carbene tool and the surface dimer. In this case the triplet state of the surface dimer is 0.07 aJ (10 kcal/mol) above the singlet state, and the triplet state of the carbene tool is 0.30 aJ (43 kcal/mol) above the singlet state. Thus, the excited state surface is about 0.37 aJ (53 kcal/mol) above the ground state surface at infinite separation. The calculations show a barrier of about 0.09 aJ (13 kcal/mol) arising from this surface crossing. These two pathways are shown in Fig. 14 and the energies are given in Table IX. Here it is seen that the bridged carbene tool is bonded to the surface by about 118 kcal/mol. Twisting the C₃H₂ moitey by 90° such that the CC p bond is broken costs 0.45 aJ (65.1 kcal/mol), while the remaining single bond is worth 0.51 aJ (73.5 kcal/mol). This is less than the energy of a bridged carbon on the surface dimer ( about 0.83 aJ (120 kcal/mol) for the carbene tool) so the CC bond between the added carbon and the departing C₃H₂ is expected to break in preference to the bond of the bridged carbon to the surface.

IV. Conclusions.

Density functional theory methods have been used to examine the interaction of the carbene and C₂ tools with a pair of radical sites on the diamond (111) surface and of the carbene tool with a dimer on the reconstructed diamond (100) surface. Calibration calculations for the reaction of vinylidene with acetylene, which is analagous to some of the systems studied here, indicate that the DFT method gives reasonable results.

On diamond (111), the carbene tool (carbenecyclopropene) is found to bond preferentially to a single radical site (on top site) rather than at a bridged site. This result is believed to arise because of the large separation ( 0.252 nm (2.52 Å) ) and resulting weak interaction between adjacent radical sites on the diamond (111) surface. For the on top site there would be no opposing forces to permit breaking the CC p bond between the added carbon and the cyclopropene moity, and the carbene tool would not useful for adding a carbon to diamond (111).

The C₂ tool, on the other hand, is found to add a bridged C₂ molecule to the diamond (111) surface through a series of steps which are overall exothermic. The carbene tool can add a carbon to the bridged C₂ molecule, leading to a bridged C₃ molecule perpendicular to the surface, once again by a series of steps which are exothermic. If another radical site is activated, the C₃ can bend over to a three fold coordinated position, with only a small barrier. Thus, this series of steps can be used to create a three fold coordinated C₃ molecule on the diamond (111) surface.

The carbene tool adds to a surface dimer on the rearranged (100) surface preferentially by a typical carbene insertion pathway involving a nearly parallel approach of the reactants (barrierless process). A C_2v constrained approach has a barrier of about 0.09 aJ (13 kcal/mol) This suggests that a mechanosynthesis process in which the C_2v constrained approach is used would encounter some significant torques on the carbene tool. The series of steps proposed (Drexler, 1992) for use of the carbene tool is found to be reasonable.

These calculations demonstrate the utility of the theory in determining which proposed mechanosynthesis reactions will be useful.

References:

Celii, F. G. and Butler, J. E. 1991 Annu Rev. Phys. Chem. 42 643-684.

Drexler, K. E 1992 Nanosystems: Molecular Machinery, Manufacturing, and Computation, Wiley.

Geis, M.W., and Angus, J.C. 1992 Scientific American October 84.

Merkle, R. C. 1994 Self replicating systems and low cost manufacturing in The Ultimate Limits of Fabrication and Measurement, M.E. Welland, J.K. Gimzewski, eds.; Kluwer, Dordrecht 25-32.

Musgrave C. B., Perry, J. K., Merkle, R. C., and Goddard, W. A. Nanotechnology 1991 2 187-195.

Walch, S. P. and Taylor, P. R 1994 J. Chem. Phys. 103 4975-4979.

Weiner, B, Skokov, S, and Frenchlach, M 1995 J. Chem. Phys. 102 5486-5491.

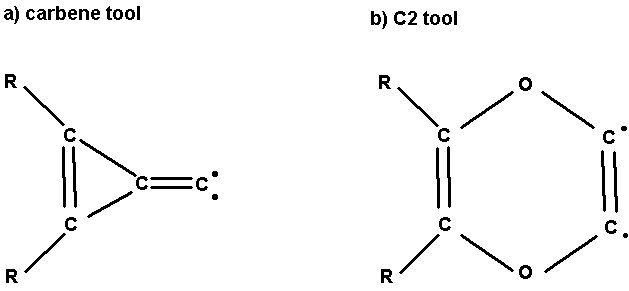
Fig. 1. The carbene tool and C₂ tool.

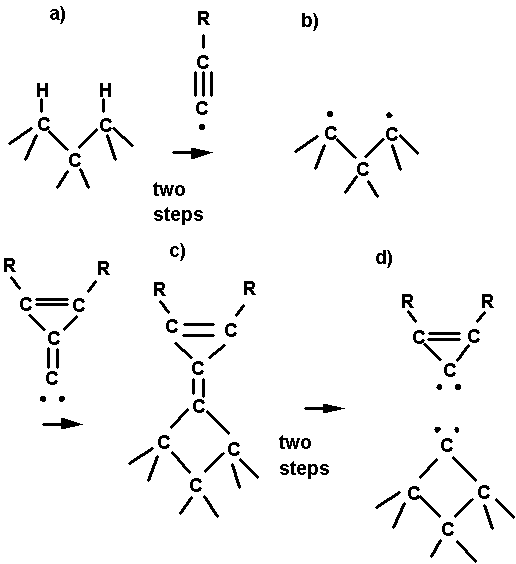
Fig. 2. A possible reaction sequence for adding a bridged carbon atom to the diamond (111) surface. The first step is abstraction of H atoms from two adjacent surface carbon atoms leading to adjacent radical sites. The next step is insertion of the carbene end of the C₂ tool leading to a bridged structure. The last step is application of torsion to break the CC p bond followed by application of force to break the remaining CC s bond.

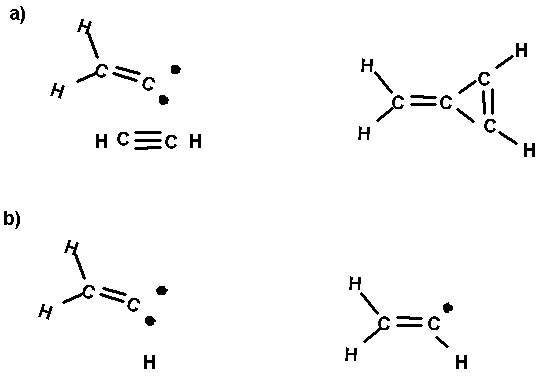
Fig. 3. Two reactions of vinylidene. a) reaction with acetylene to give a cyclopropene structure. b) reaction with H atom to give vinyl radical. These reactions are prototypes for addition of the carbene tool to give bridged and on top sites, respectively.

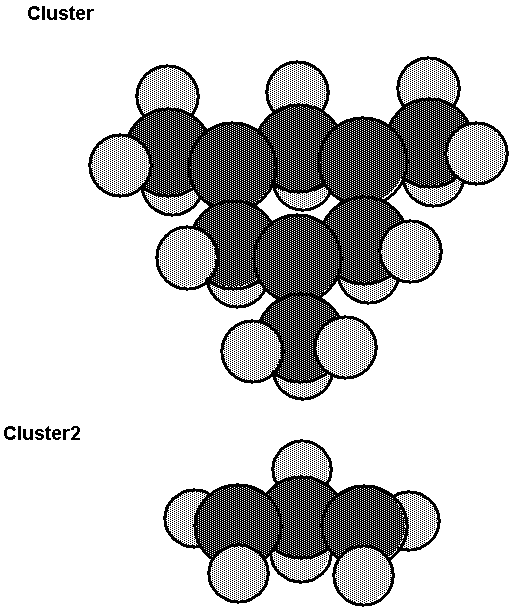
Fig. 4. Two clusters which were used to model the diamond (111) surface. The larger cluster (denoted as cluster) has three surface carbon atoms, while the smaller cluster (denoted as cluster2) has two surface carbon atoms. The atoms are fixed at the locations for the unreconstructed surface.

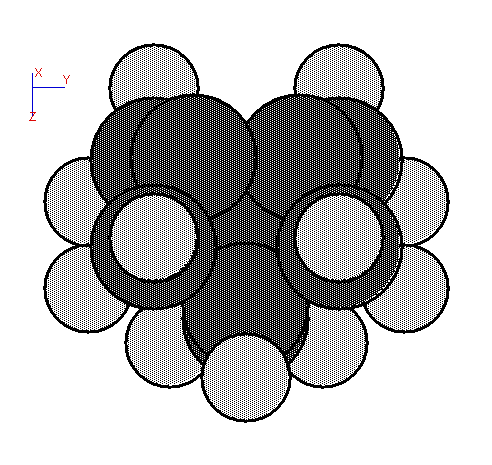
Fig. 5. Cluster for a dimer on diamond (100).

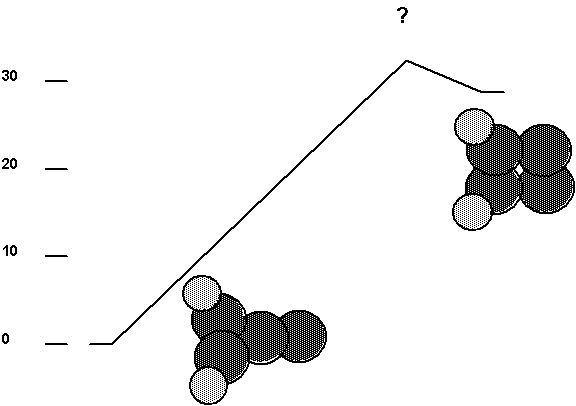
Fig. 6. Isomerization pathway for the carbene tool. The barrier height has not been determined but is greater than the endothermicity. The ordinate is energy in kcal/mol (one kcal/mol=0.00694 aJ). The same energy units are used in the remaining figures.

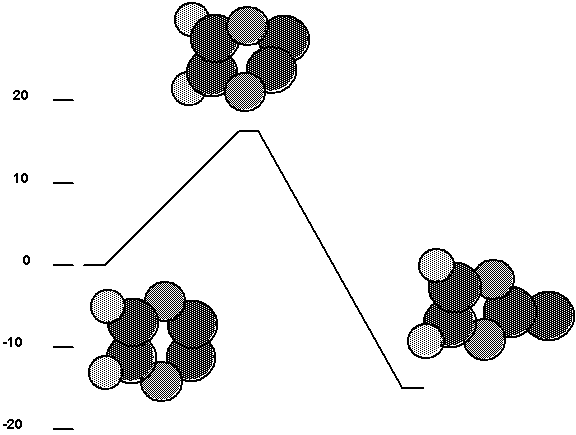
Fig. 7. Isomerization pathway for the C₂ tool.

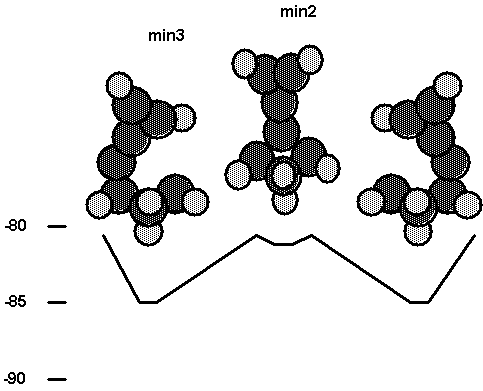
Fig. 8. Energetics for the interaction of the carbene tool with cluster2.

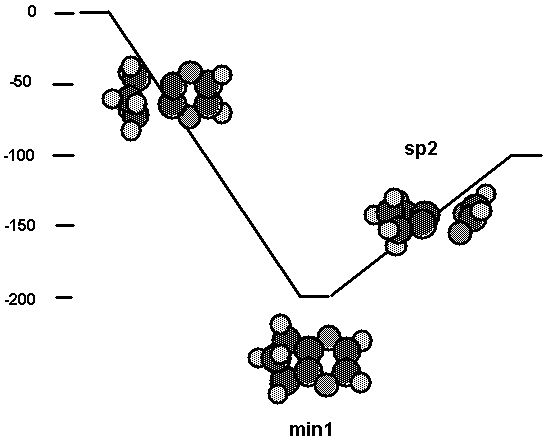
Fig. 9. Energetics for interaction of the C₂ tool with cluster2.

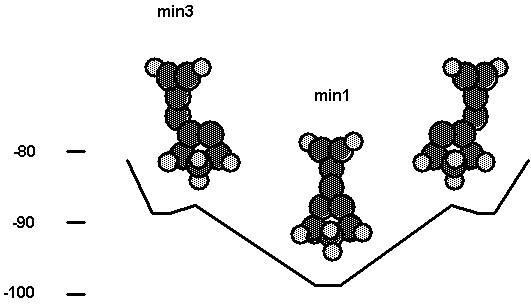
Fig. 10. Energetics for the interaction of the C₂ tool with a C₂ molecule bridged across two radical sites on cluster2.

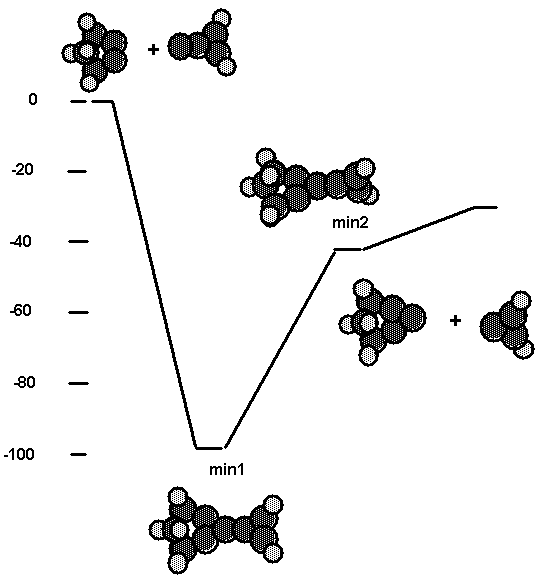
Fig. 11. Energetics for the reaction of the C₂ tool with a C₂ molecule bridged across two radical sites on cluster2. The product is a C₃ molecule sitting perpendicular to the surface.

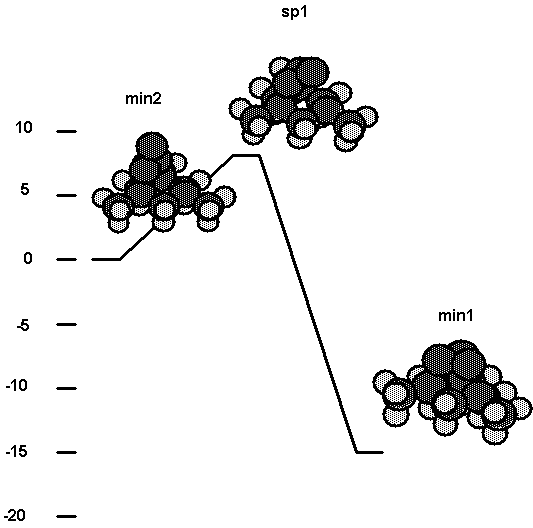
Fig. 12. Energetics for a bridged C₃ molecule interacting with an adjacent radical site. The product is a three fold coordinated C₃ molecule.

Fig. 13. Minimum energy pathway for insertion of the carbene tool into a surface dimer on the reconstructed diamond (100) surface. The energies (in kcal/mol) with respect to carbene tool plus the cluster are also given.

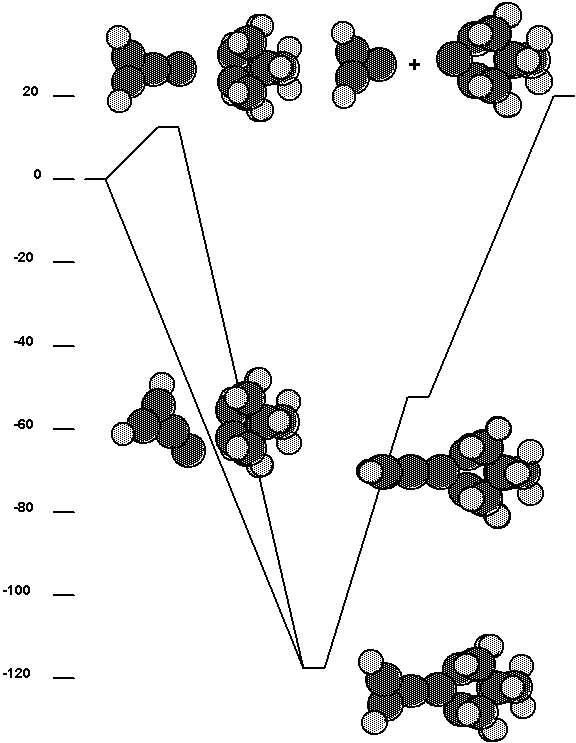
Fig. 14. Energetics for the c2 tool plus a surface dimer on the reconstructed diamond (100) surface.

Table I. Energetics for isomers of C₄H₂. (carbene tool)

structure	ICCI(ICCI +Q +152.)^a	ZPE^b	DE^c
carbenecyclopropene	-152.90656(-.96332)	.036514	0.0
1,2-dehydrocyclobutadiene	-152.85853(-.91750)	.037702	0.20

^a ICCI is internally contracted CI, ICCI +Q is internally contracted CI plus a multireference Davidson's correction.

^b zero-point vibrational energy estimated from the CASSCF harmonic frequencies.

^c Energy difference (aJ) including correction for zero-point energy.

d. Unless indicated otherwise all energies are in E_H ( one E_H =4.359 748 2 x 10^-18 J). The same convention is used for the remaining tables.

Table II. Energetics for isomers of C₄O₂H₂. (C₂ tool)

structure	ICCI(ICCI+Q+ 302.)	ZPE	DE^a
min1	-302.79852(-0.89419)	.051756	0.0
sp	-302.76198(-0.86500)	.048373	0.11
min2	-302.82217(-0.91752)	.051101	-0.10

^a Energy difference (aJ) including correction for zero-point

Table III. Energetics for vinylidene + acetylene.

	DFT			Ab Initio
structure	Energy	ZPE^a	DE^b	DE^b
acetylene	-77.31201	.02724
vinylidene	-77.24135	.02437
	-154.55336	.05161	0.0	0.0
sp1	-154.55368	.05462	0.01	0.04
min2	-154.65561	.06137	-0.40	-0.37

^a zero-point vibrational energy estimated from the DFT harmonic frequencies.

^b Energy difference (aJ) including correction for zero-point

Table IV. Energetics for CH₃ + vinylidene (pDZ optimized structures).

structure	ICCI(ICCI +Q +116.)^a	ZPE^b	DE^c
CH3 + CCH2	-116.73157(-.77535)	.055247	0.0
CH3-CCH2 SP	-116.73373(-.77897)	.059325	0.002

^a ICCI is internally contracted CI, ICCI +Q is internally contracted CI plus a multireference Davidson's correction.

^b zero-point vibrational energy estimated from the CASSCF harmonic frequencies.

^c Energy difference (aJ) including correction for zero-point

Table Va. Cluster2 + C₄H₂ Energetics.

structure	DFT	DE^a
cluster2 + H	-118.43037
C4H2	-153.32306
	-271.75343	0.0
min1	-271.88691	-0.58
cluster2	-117.74505
C4H2	-153.32306
	-271.06811	0.0
min2	-271.19816	-0.57
min3	-271.20344	-0.59

^a Energy difference (aJ).

Table Vb. Cluster + C₄H₂ Energetics.

structure	DFT	DE^a
cluster +2H	-353.05775
C4H2	-153.32306
	-506.50457	0.0
min1	-506.504568	-0.54
cluster + H	-352.38179
C4H2	-153.32306
	-505.70485	0.0
min2	-505.81816	-0.49
min3	-505.83054	-0.55

^a Energy difference (aJ).

Table VIa. Cluster2 + C₂tool Energetics.

structure	DFT	DE^a
cluster2	-117.74505
c2tool	-303.70708
	-421.45213	0.0
min1	-421.77051	-1.39
sp2	-421.60813	-0.68
cluster2 + C2	-193.87682
glyoxal	-227.73297
	-421.60979	-0.69

^a Energy difference (aJ).

Table VIb. Cluster + C₂tool Energetics.

structure	DFT	DE^a
cluster + H	-352.38179
c2tool	-303.70708
	-656.08887	0.0
min1	-656.38747	-1.30
cluster +H + C2	-428.50013
glyoxal	-227.73297
	-656.23310	-0.63

^a Energy difference (aJ).

Table VII. Cluster2 + C₂ + C₄H₂ Energetics.

structure	DFT	DE^a
cluster2 + C2	-193.876819
C4H2	-153.32306
	-347.19988	0.0
min1	-347.35530	-0.68
min2	-347.26911	-0.30
cluster2 + C3	-231.94487
C3H2	-115.30456
	-347.24943	-0.22
min3	-347.34152	-0.62

^a Energy difference (aJ).

Table VIII. Cluster + C₃.

structure	DFT	DE^a
min2	-465.89186	0.0
sp1	-465.87846	0.06
min1	-465.91599	-0.10

^a Energy difference (aJ).

Table IX. Energetics for diamond 100 + carbene tool.

structure	DFT	DE^a
cluster100	-349.90617
carbene tool	-153.32306
	-503.22923	0.0
min1	-503.41654	-0.82
twisted	-503.31265	-0.36
cluster100+c	-387.89108
C3H2	-115.30456
	-503.19564	0.15

^a Energy difference (aJ).